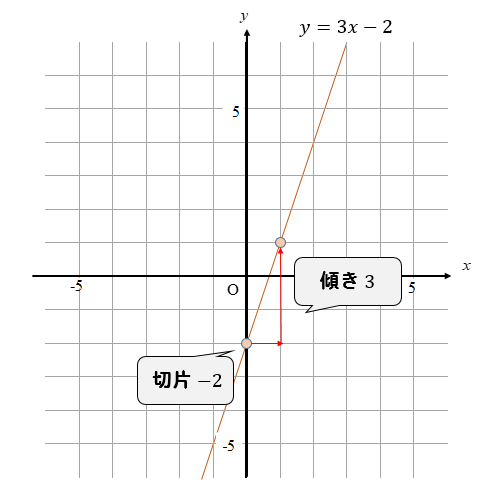
Excelを用いた連立方程式の解法 このページでは,Excel関数を使って連立方程式を解く手順について解説する. 手順 連立方程式を行列で表現し,行列Aと行列Cの係数をExcelシートに入力する.一次関数のグラフに は傾きや切片がある んだ。 さおばかり 式 切 片は空のケースの重 さなんだ。 連立方程式の解はそ のグラフの交点にな るんだ。 ともなって変わる関係を式やグラフにすればわかりやすい。 一次関数を利用して,時間と道のりや携放物線と直線の交点は 連立方程式を解く! ですね(^^) 連立方程式を解くときには、二次方程式の解法も必要になってきます。 計算に不安がある方は、方程式の練習もしておきましょう! 二次方程式問題の解説付き!解き方をパターン別に説明していく
連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト
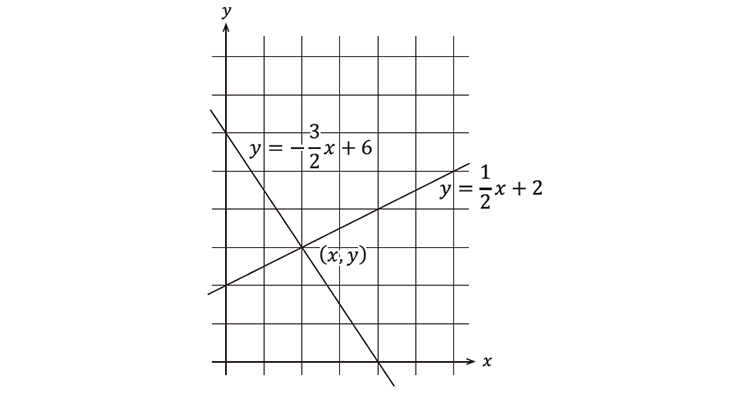
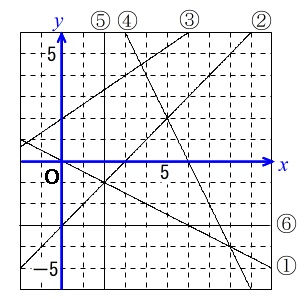
連立方程式 グラフ 交点
連立方程式 グラフ 交点-しかし、これら2つの二元一次方程式を同時に満たす解は、1つしかありません。 それは、x=2 のとき y=5 という解です。 これを簡単に求める方法が「連立方程式」なのです。 今度は、グラフに目を向けます。 y=2x1 のグラフですが、 このグラフ、実は授業実践記録(数学) 1.単元名 ~お得な携帯電話プランをつくろう(「一次関数」「連立方程式」)~ 2.単元設定の意図 (1)単元について 数量の関係を日常生活の中から見つけ出し,「一次」の概念を式や表,グラフなどを用いて総合的に獲得して




中学2年生の数学 連立方程式とグラフ です 解説を見てもよくわからないので もっと詳 Clear
連立方程式とグラフ ・連立方程式の解は2直線の交点の座標であることを見い出し,連立方程式を利用して2直線の交点の座標を求めることができる。 ・連立方程式を利用して,簡単な2直線の交点の座標を求めることができる。方程式 axby=c のグラフは,a=0 のときx軸に平行な直線になり,b=0 のときy 軸に平行な直線になる。 2 連立方程式とグラフ 2つの2元1次方程式のグラフの交点のx座標,y座標の組は,その2つの方程式を 組にした連立方程式の解である。 覚えよう! x y O y= x= b c b cグラフで解く連立方程式 中学校では、2年生で、 のような、2元連立一次方程式を学ぶ。代入法とか加減法により、その解き方が指導され る。 グラフを用いた次のような解法もよく知られている。
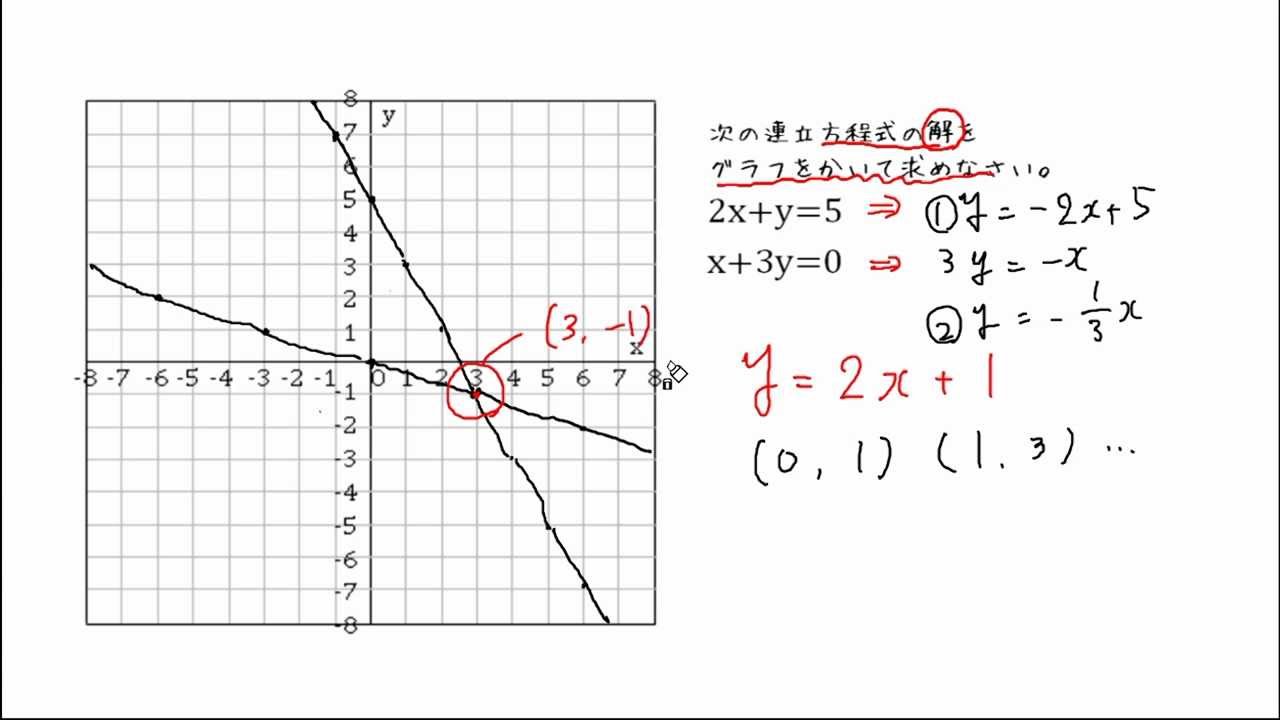
連立方程式の解とグラフ 2元1次方程式のグラフは直線になるので,連立方程式の解 とグラフについては,次のことがいえる。 • それぞれの方程式のグラフの交点のx 座標,y 座標が, 連立方程式の解アより,y=-3x-2 イより,y=x+2 グラフの 交点は(-1,1) x=-1,y=1 次の直線アとイの交点の座標を,計算で求めなさい。 3 ア y=2x+1 イ y=-x+4 連立方程式をつくると連立方程式の解は①と②のグラフの交点のχ座標、y座標の組だから χ=2 答. y=-2 →52へ 問1 χ+y=5 ① 連立方程式 について、 2χ-y=4② 次の問いに答えなさい。 (1)方程式①、②のグラフをかきなさい。 χ+y=5をyについて解くと
グラフから読み取れない パターンの問題が多い!! ①グラフから式を読み取る力 ②連立方程式を使って交点を 求められる計算力 この2つの力が必要!2直線の交点を求めましょう。交点とは直線どうしが交差する点です。 直線は2点(始点と終点)の座標(x、y)で表現できます。 直線1 始点(x1s, y1s) 終点(x1e,y1e) 直線2 始点(x2s, y2s) 終点(y2e,y2e) とする。 直線1の方程式は-グラフの交点の座標を連立方程式を使って求めることができるようになろう-p 学習日 月 日 年 組 番 氏名 x y x y 1 連立方程式 2x-y=2 を, x+y=4 グラフを利用して次の手順で解いた。 (1) 空らんにあてはまる数を入れ,グラフ
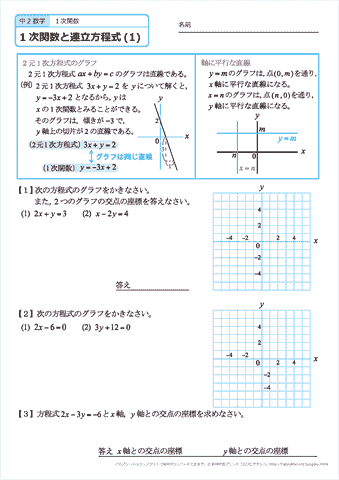



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1
連立方程式 (1) (2)の解は,2つの方程式 (1) (2)を両方とも満たすものですが,これはグラフで考えれば両方の直線上にある点ということになります. したがって,連立方程式の解は2直線の交点の座標になります. ※それぞれの直線は「傾きと切片を指定する Contents1 問題2 ポイント3 解き方31 ステップ1 2つの式を「y=ほにゃらら」の形に変形する32 ステップ2 実際にグラフを書く33 ステップ3 グラフから交点を読み取る 問題 連立方程式連立方程式を利用してグラフの交点の座標を求めたりすることができる。 (4)一次関数,変化の割合,傾きと切片,二元一次方程式のグラフの意味について理解する。 4単元の指導計画(全19時間) 節 項 時 主な内容 §1一次関数 1 ・一次関数の定義(本時)




直線の交点の座標を求める 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
方程式。関数。 どちらも中学生になってから学ぶ範囲です。 そして、世の中学生、高校生たちを「数学嫌い」に陥らせる一番の原因でもあります。 まず数学が嫌いになる子は「文字式」の扱いから頭がこんがらがってしまい、考えることを終了してしまうのですが、そんな手痛い洗礼をねらい ・ 2直線の交点の座標は、それを組とする連立方程式の解と一致することを理解する。 ・ 2直線の交点の座標は、連立方程式の解になっているとみることができる。 段階 学習活動数学的活動を通した 指導のポイント つかむ ・方程式 x + y円の方程式~平方完成形~ 無題 円は,中心と半径を決めればただ1つに定まる. そこで,座標平面上の点 (a, b) を中心とした半径 r の円 C は, どのような方程式で表されるか考えてみよう. 円 C の周上にある点 P の座標を (x, y) とすると, 2点 A, P 距離は




一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく
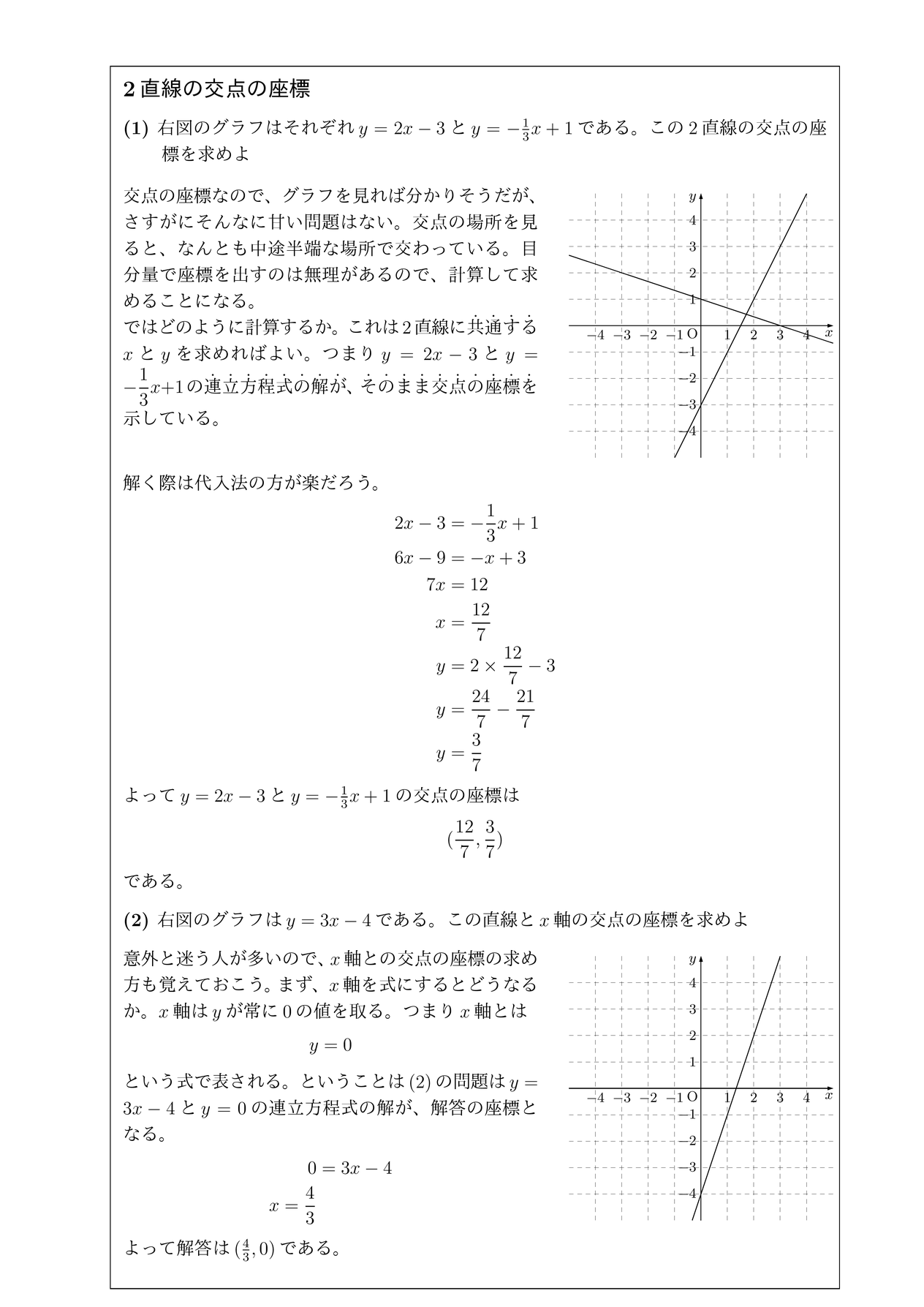



2直線の交点の座標 チーム エン
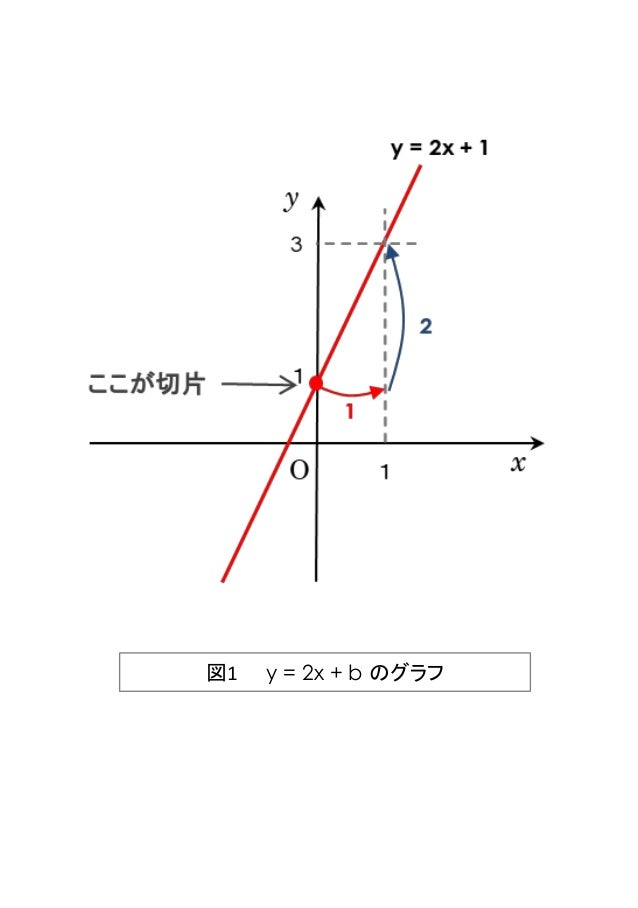
の2つの方程式をグラフにしてみると、こうなるね ↓↓ ここからが勝負さ! Step2 直線の交点をこの交点の座標を求めるには、 グラフの交点の座標(x,y)は、2つの式を両方とも満たす という性質を利用するんだ。 つまり「2つの式を連立した方程式の解(x,y)」が「グラフの交点の座標(x,y)」になるんだね。連立1次方程式の解のグラフ的な意味につい て理解させるために, 1次方程式に対応する直 線の交点として,解を理解させるのである。 中学校で出てくる解は整数解であることが多 く,格子点が書かれた座標に方程式に対応する




1次関数のグラフの応用 3種類の交点とグラフ上の面積 教遊者




Eca 13 8 Itimes 7 2 11 Descubre Como Resolverlo En Qanda
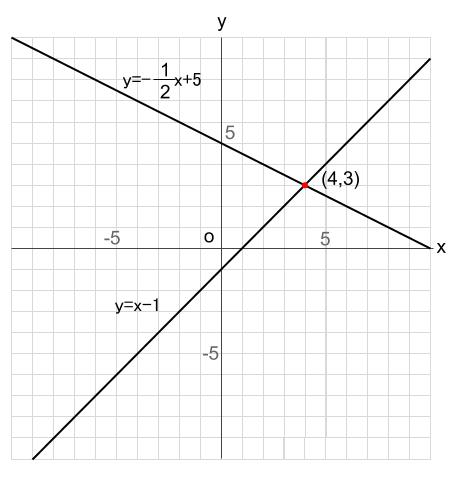
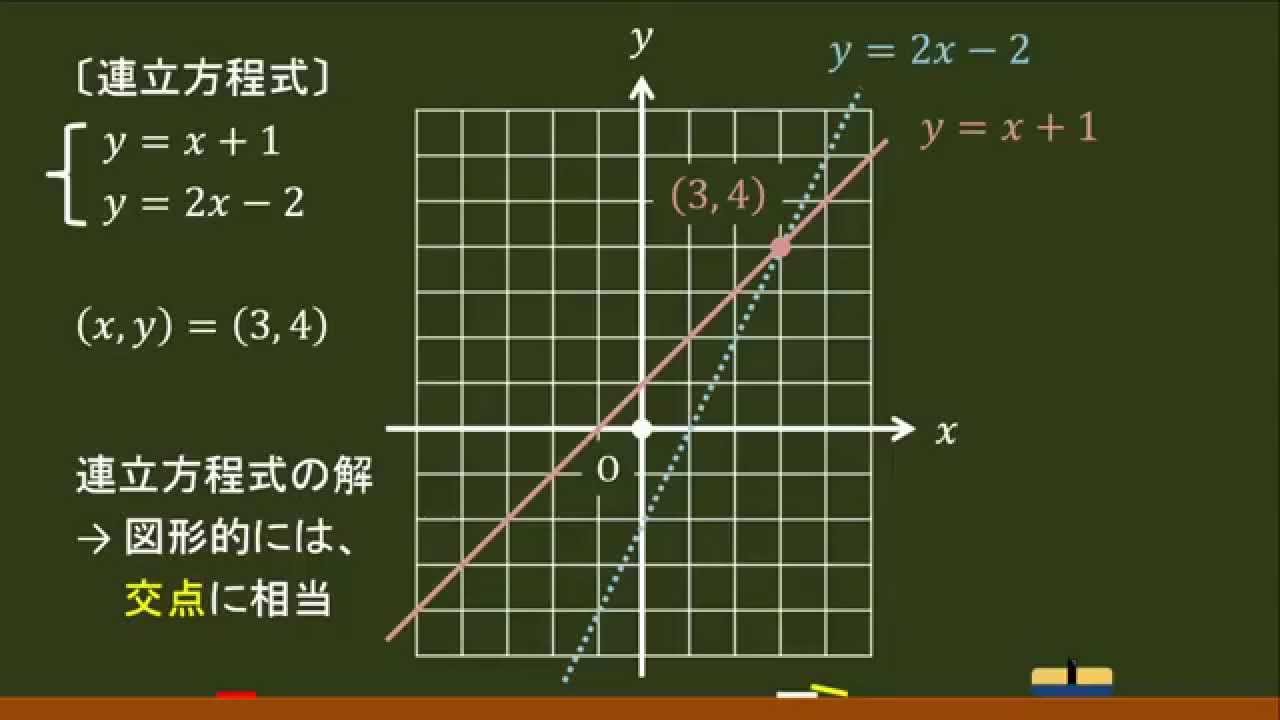
連立方程式の解とそのグラフの交点の座標との関係 グラフの交点の座標の意味するもの 2つの方程式,x +y =7 ① y -2x =-5 ② のグラフを書いた時,交点の座標は(4 ,3 )である このとき,交点の座標は, ①,②を連立方程式としてみたときの解をそれぞれの式を連立方程式で解いたときに出てくる解と等しくなります。 なので、2直線の交点を問われば 連立方程式を解くべし! ということで $$\begin{eqnarray} \left\{ \begin{array}{l}y=2x1 \\y=x2 \end{array} \right \end{eqnarray}$$ この連立方程式を解いていきましょう。2 連立方程式と グラフ 〇連立方程式の解とその グラフの交点の座標と の関係について理解し ようとしている。 〇交点を求める際に,連立 方程式を代入法を使う などして,効率よく解く ことができる。 〇2直線の交点の座標を, 連立方程式を用いて求 め



連立方程式とグラフ 中学から数学だいすき



問題3 連立方程式を解くプログラムを作れますか Pythonで学び直す高校数学 エンジニアtype 転職type
6 連立方程式とグラフの関係につ いて調べる。 ・連立方程式の解とそのグラフの 交点の座標との関係 ・2直線の交点の座標を,連立方程 式を用いて求めること 二元一次方程式と一次関 数の関係に気づかせるた めに,二元一次方程式と(10) 連立方程式とグラフ 学習日 月 日( ) 連立方程式の解 ⇔ 方程式のグラフ(直線)の交点の座標 次の2直線の交点の座標を求めなさい。・連立方程式の解とグラフの交点の関係を理解している。 4 単元の指導計画( 総時間数 15 時間 ) 主な学習活動・内容 主な指導・支援上の留意点 評価規準(評価方法)



連立方程式とグラフ まなびの学園




中2数学 グラフの交点と連立方程式の解 5分で学習 Youtube
二元一次方程式のグラフを理解し,そのグラフをかいたり, 2直線の交点を求めたりることができる。 ・二元一次方程式のグラフをかく。 ・連立方程式を用いて,2直線の交点を求める。 数学的な見方ここでは連立方程式を使って、2つの解答を出すパターンを行いま す。この計算は、以下のような2つのグラフの交点で示される均衡価格 と均衡需給量を求める場合などに使われます。 aさん 0 需給量 価格 供給曲線(s) 需要曲線(d) (d、s) (p) 考え方X y = 3;



連立方程式と一次関数 名古屋市北区の学習塾は思考力を育む 泰成スクール



連立方程式とグラフ
3 連立方程式とグラフ x,yについての連立方程式の解は,それぞれの方程式のグラフの交点の座標と一致する。 x k h y O y=k x=h 教科書 単元 14 一次関数と方程式 P77〜 啓林 _1_Keyワーク_数学_啓林_2年_Qindd 78 1714 連立方程式を解くには、PythonのライブラリであるSympyのsolve ()関数を使います。Pythonインタプリタで以下のように実行してみると、交点の座標が(2, 3)であることがわかります。 ※Pythonインタプリタの使い方は第2回「方程式をもとにPythonでグラフを描いてなぜ、連立方程式の解が、グラか。 フの交点の座標になるのかを考え 研究視点2 る。 8 まとめ 連立方程式の解を、方程式のグラフの交点の座標を読み取ることで求めることができる。 9 評価問題を解く。




2 2 2 D 0 22 D424 22 Descubre Como Resolverlo En Qanda




中2数学 1次関数と連立方程式 映像授業のtry It トライイット
「連立方程式と一次関数のグラフとの関係」 1 出題の趣旨 連立二元一次方程式の解は,グラフに表した座標平面上の2直線の交点の座標とし て求められることを理解しているかどうかをみる。連立方程式の解とグ ラフ(グラフの交点) 軸に平行なグラフ aχbyc=0 のグラフ グラフをかく② ・2点を使って 式を求める③ ・2点(2組のχ とyの値)から グラフの利用 ―変域の対応― 式を求める② ・1点(1組のχとy の値)と傾きから 関数について Step1 方程式のグラフを2つかく! 方程式のグラフを2つかこう。 かき方を忘れたときは、 「方程式とグラフ」を復習してみてね。 例題の、 3x y = 5;



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su




2つの直線の交点の座標の求め方 中学数学 By じょばんに マナペディア



エクセルを用いた2直線の交点計算



数学教材 中間発表



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su




一次関数の問題の解き方 7パターン 数学fun



Q Tbn And9gctcj6w5hlvl3fax2o1sigai Pbco1qvgoabehcatlhvalcryvqe Usqp Cau
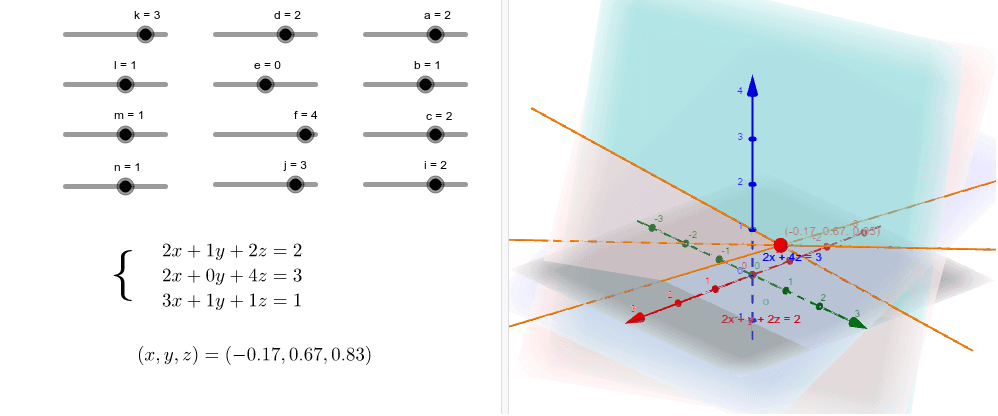



三元一次連立方程式 Geogebra



連立方程式とグラフ 中学2年 数学クラブ
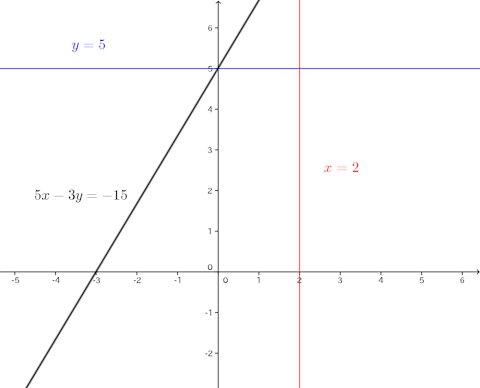



ねこ騙し数学
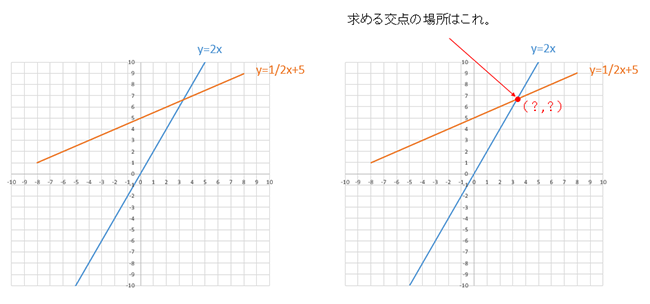



2直線の交点座標を連立方程式で求める方法 図解で超カンタンまとめ My Terrace マイテラス




中学2年生 交点の座標を求めるに ついて Okwave




一次関数の問題です 教えれる人は が付いた問題を1つずつ教えてください よろしくお願 Clear



1次関数の交点の座標とグラフから直線の方程式を求める方法



放物線と直線 交点の座標の求め方とは 解き方を問題解説 数スタ




中3数学 2次関数 連立方程式とグラフ 面積を求める オンライン無料塾 ターンナップ




中2数学 一次関数と方程式 グラフの交点から連立方程式の解を求める 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト




曲線の交点 数学i フリー教材開発コミュニティ Ftext



放物線と直線 すうがく先生




けーご 1日1青チャート生活 95日目 一題のみ 二つの二次方程式のグラフの交点をだすやつ 連立方程式やれば余裕なんよ ただ解が二つずつ出るからそこだけ気をつけんといかん




問題の解き方がわかりません どなたか教えてください Clear
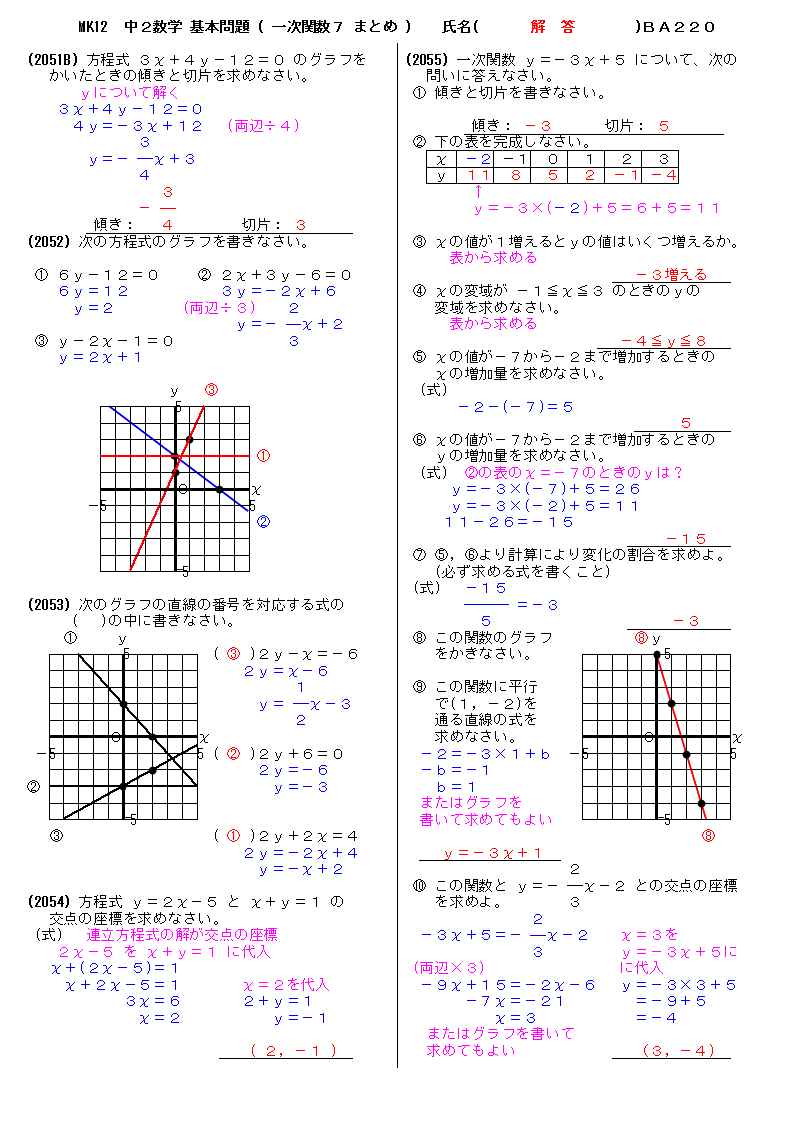



無料 中2数学 基本問題 解答プリント 2 一次関数7 まとめ



連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト
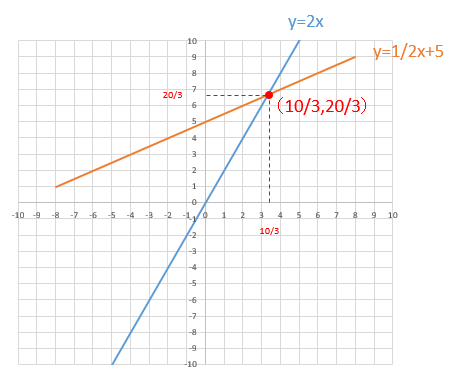



2直線の交点座標を連立方程式で求める方法 図解で超カンタンまとめ My Terrace マイテラス



連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト



中2数字です この問題で 普通に連立方程式をといて そのまま交点と結ぶの Yahoo 知恵袋



1
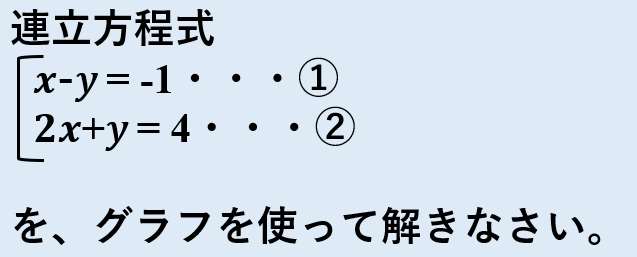



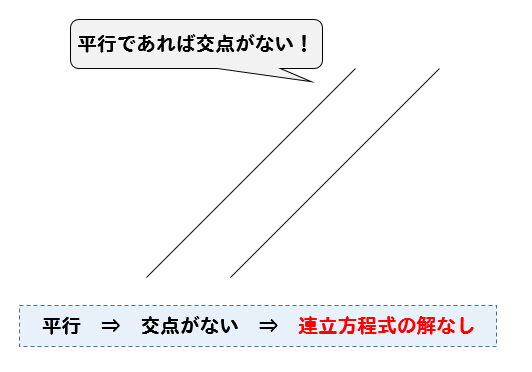
中2数学 一次関数と方程式 グラフの交点から連立方程式の解を求める 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




中学2年生の数学 連立方程式とグラフ です 解説を見てもよくわからないので もっと詳 Clear
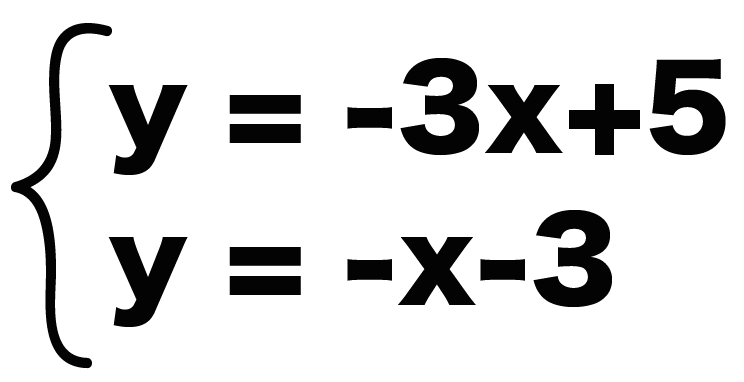



2直線の交点の座標の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



数学 1次関数 連立方程式とグラフ 1次と1次 オンライン無料塾 ターンナップ Youtube



一次関数と連立方程式 Youtube



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su




こんな風に なぜ連立方程式で交点がわかるんですか Clear




解き方を教えて下さると嬉しいです お願いします Clear
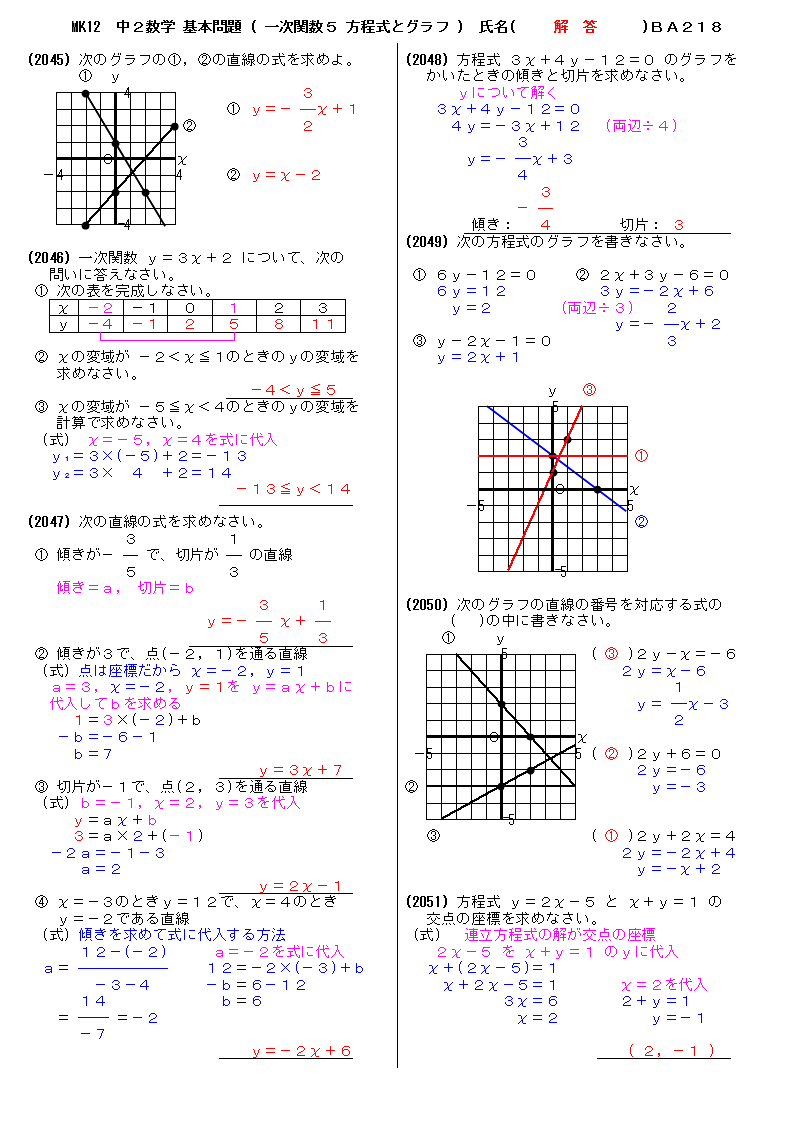



無料 中2数学 基本問題 解答プリント 218 一次関数5 方程式とグラフ



画像のグラフでについてです この図の2直線 の交点の座標を求めな Yahoo 知恵袋



中3数学二つの一次関数のグラフの交点は連立方程式のかいをあらわして Yahoo 知恵袋
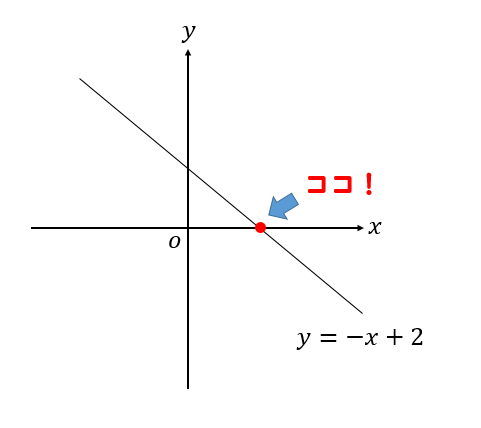



一次関数 座標の求め方は いろんな座標を求める問題について解説 数スタ
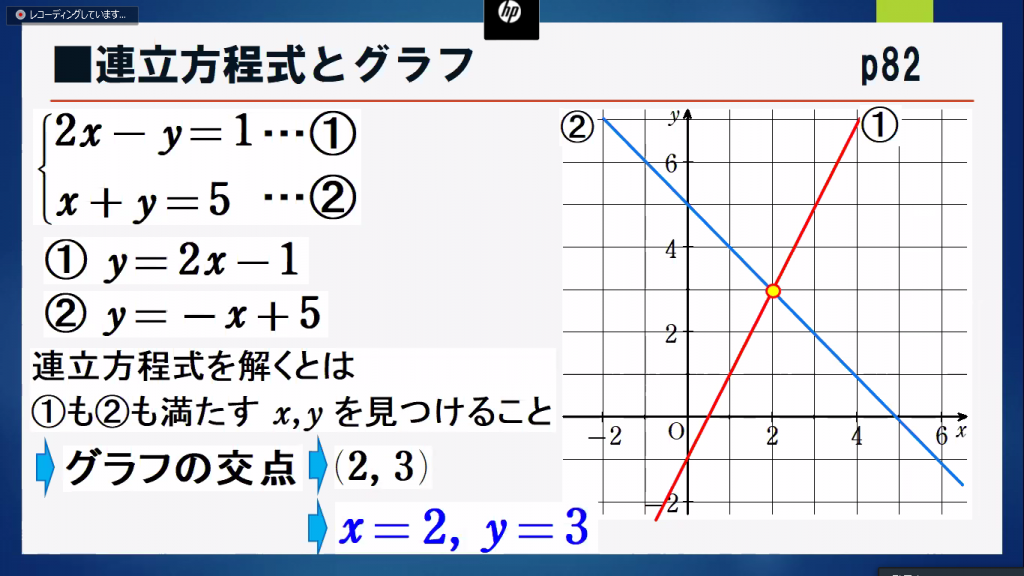



オンライン授業の様子 5月27日 和洋九段女子中学校高等学校
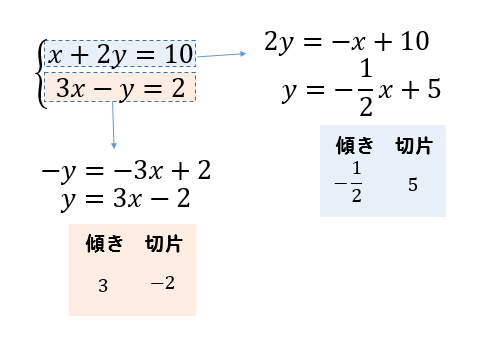



連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト




一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 リョースケ大学




2数 連立方程式の解とグラフの交点 Youtube



Http Www Fdtext Com Dat Suub2 3kansuu 1gurafu Pdf
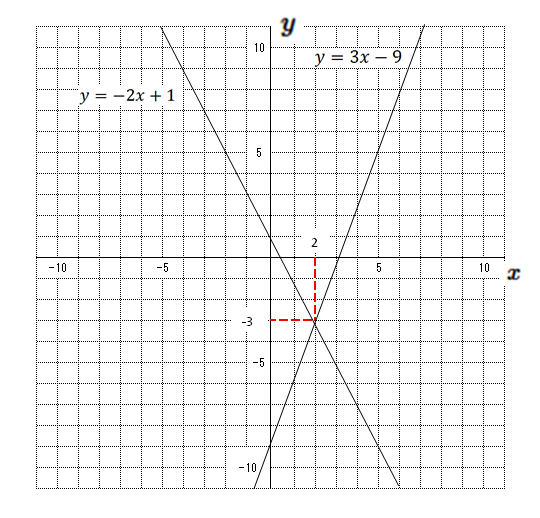



一次関数と連立方程式 1 ネット塾
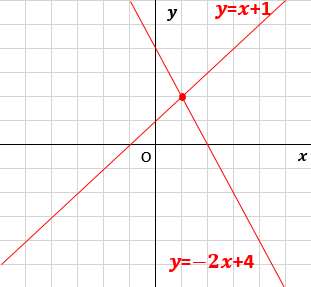



中2数学 一次関数と方程式 グラフの交点から連立方程式の解を求める 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張



2直線の交点の座標の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
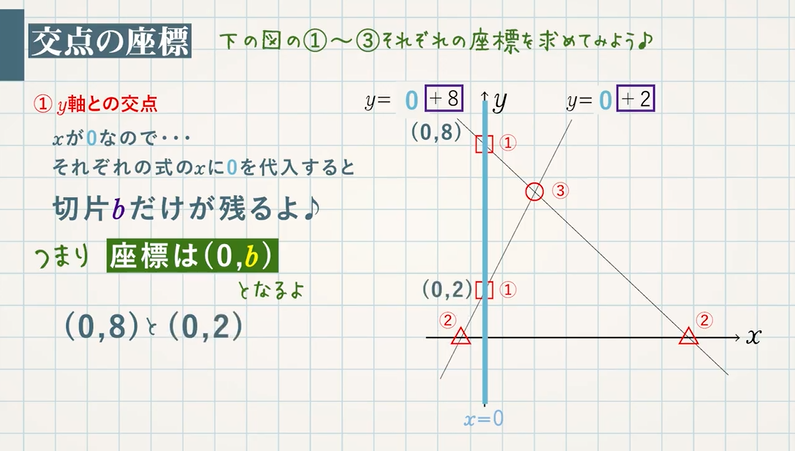



1次関数のグラフの応用 3種類の交点とグラフ上の面積 教遊者



Excelでこのようなグラフの交点を求める方法を教えて下さい Yahoo 知恵袋
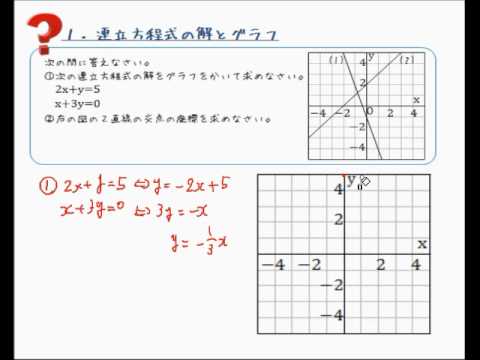



連立方程式の解とグラフ Youtube
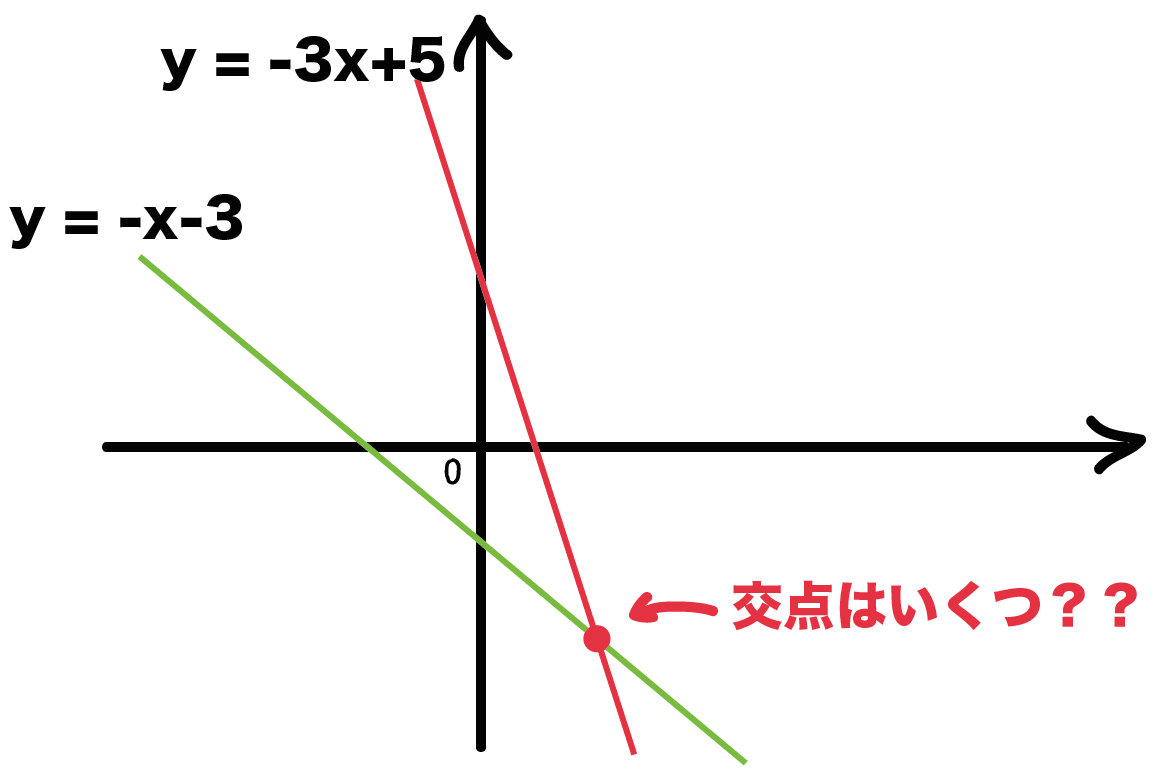



2直線の交点の座標の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




連立方程式の解き方と交点の座標の求め方 数学の偏差値を上げて合格を目指す



1




Maximaで方程式 連立方程式を解く 数列を求める Pianofisica




一次関数のグラフの利用1 無料で使える中学学習プリント
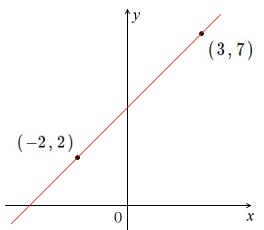



1次関数の交点の座標とグラフから直線の方程式を求める方法




連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト




中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




21 1164 1 3y122 2 2 3 Descubre Como Resolverlo En Qanda
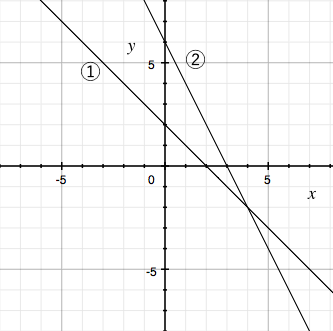



一次関数 連立方程式とグラフの関係 苦手な数学を簡単に
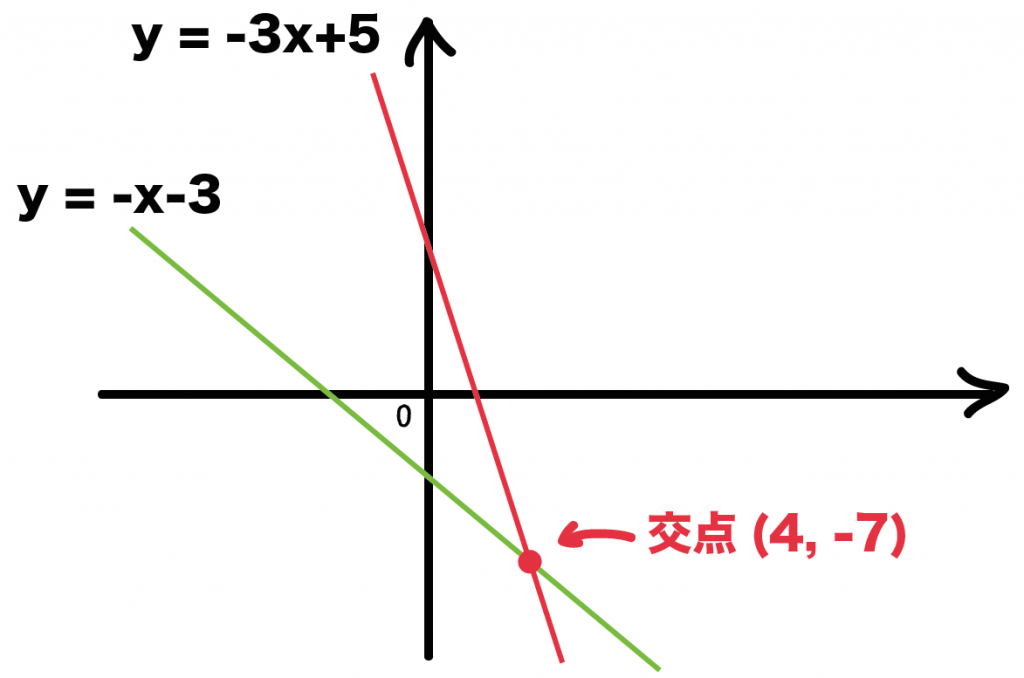



2直線の交点の座標の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



できる人の関数グラフの解き方 教遊者




中2数学講座第3章1次関数 9 連立方程式の解とグラフ基本問題 Youtube




数学 中2 36 一次関数の交点をだす 基本編 Youtube




一次関数 連立方程式とグラフの関係 苦手な数学を簡単に



2




連立方程式の グラフを用いた解き方について 次の連立方程式を 数学 教えて Goo




1次関数のグラフの応用 3種類の交点とグラフ上の面積 教遊者
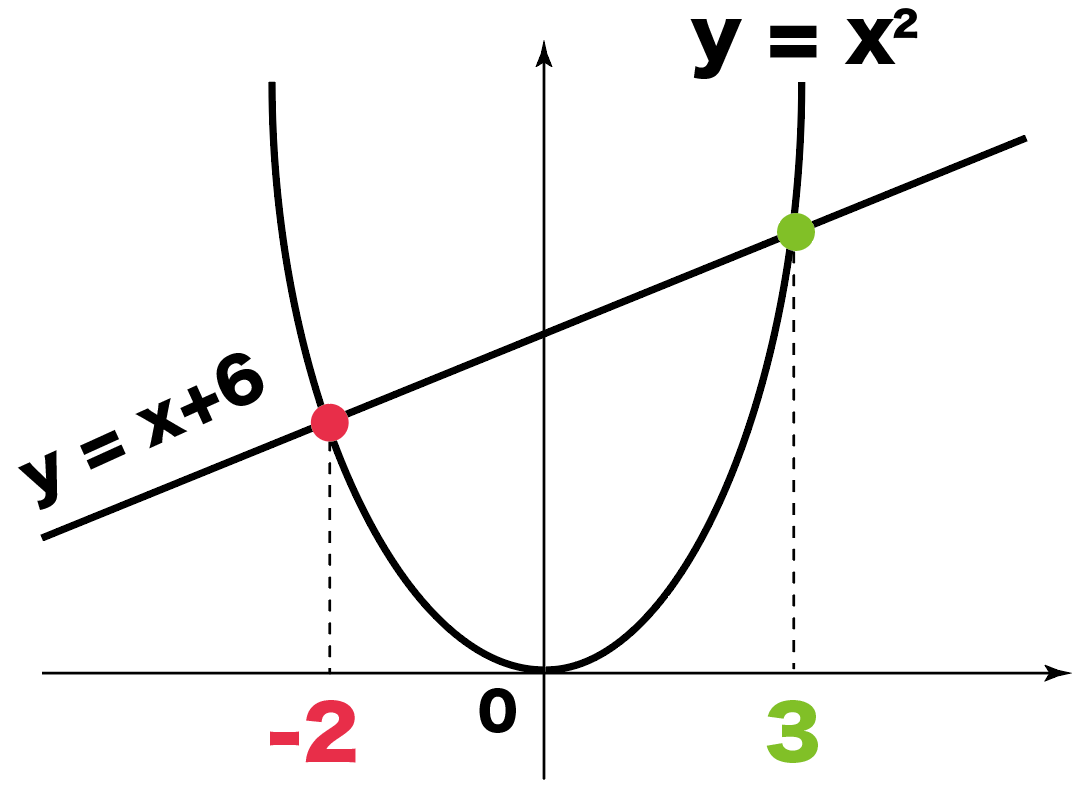



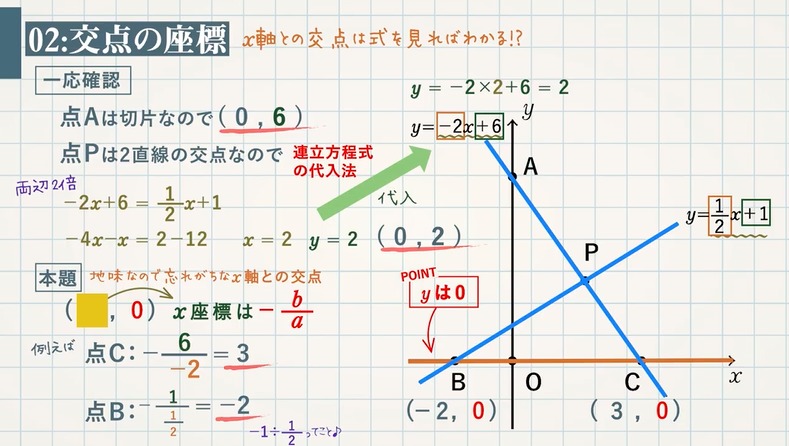
一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




なぜグラフがこのようになるんですか Clear



Www City Hadano Kanagawa Jp Www Contents Simple B053a Pdf



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su




2 Left 1right 2 Y Descubre Como Resolverlo En Qanda
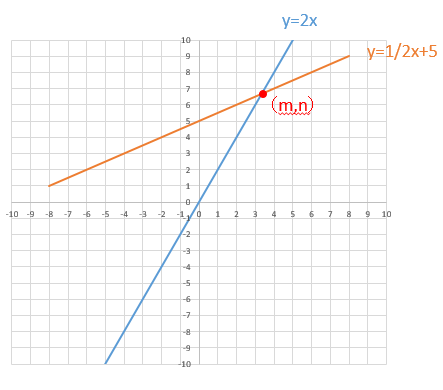



2直線の交点座標を連立方程式で求める方法 図解で超カンタンまとめ My Terrace マイテラス



連立方程式とグラフ
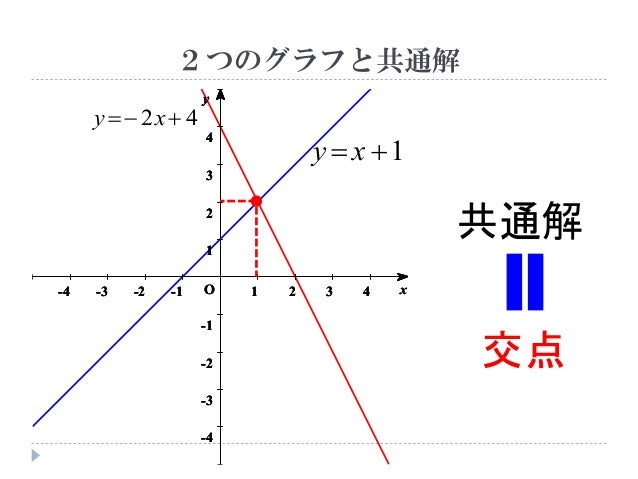



連立方程式 連立方程式とグラフ
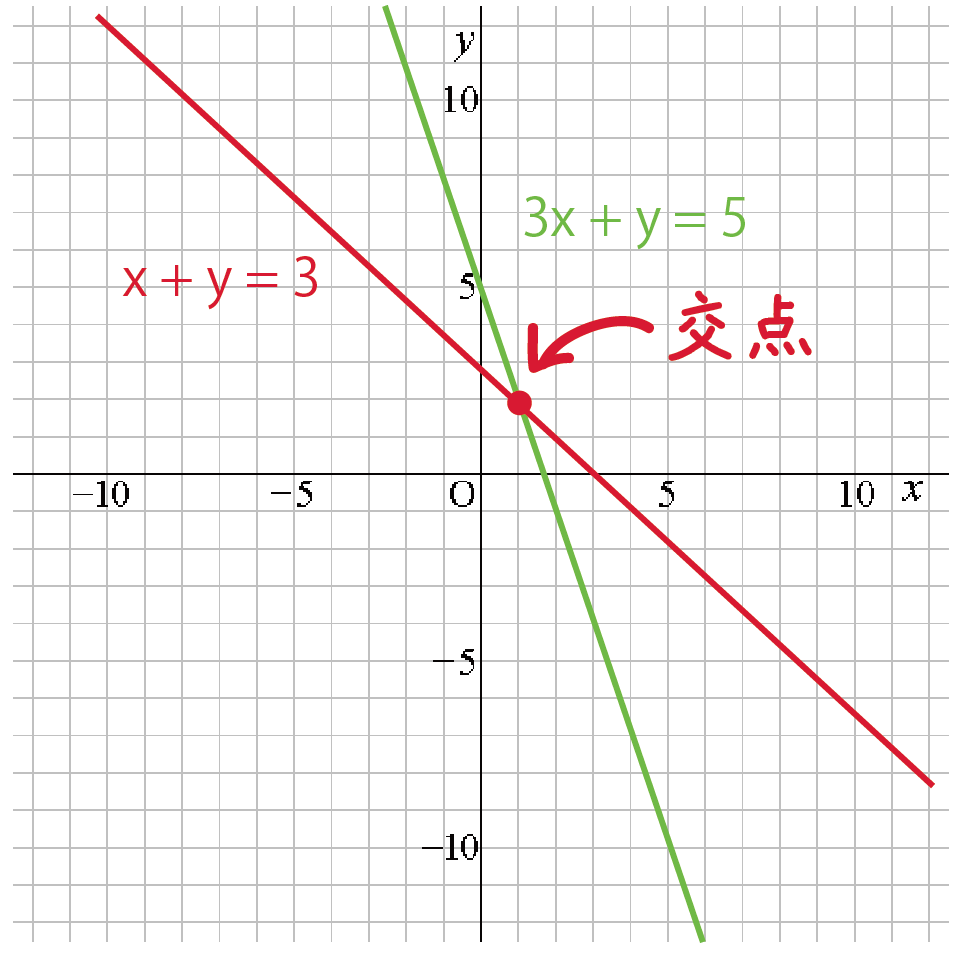



一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく
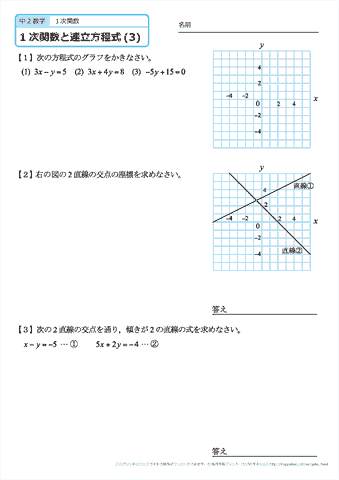



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
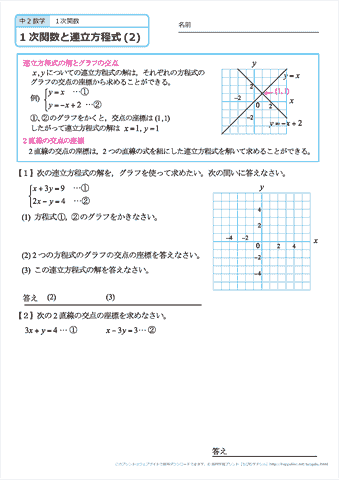



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
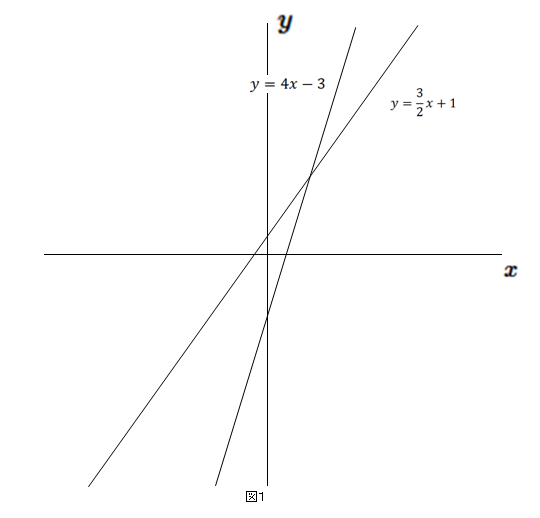



一次関数と連立方程式 2 ネット塾




一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 リョースケ大学
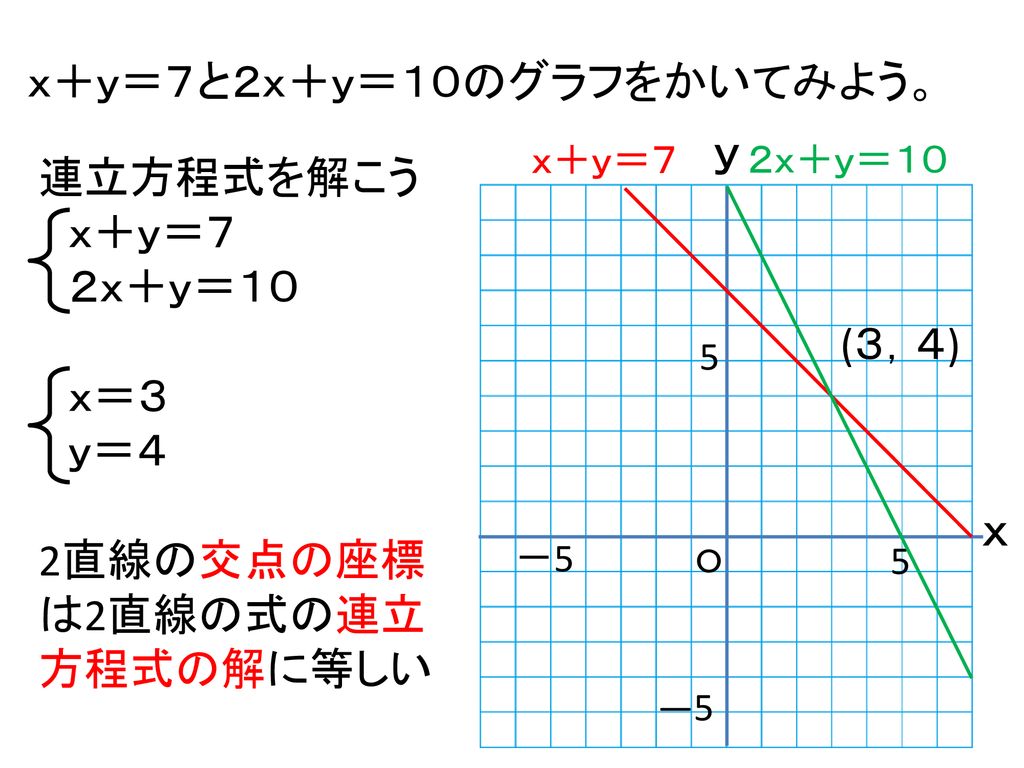



ねらい 連立方程式とグラフの関係について理解する Ppt Download
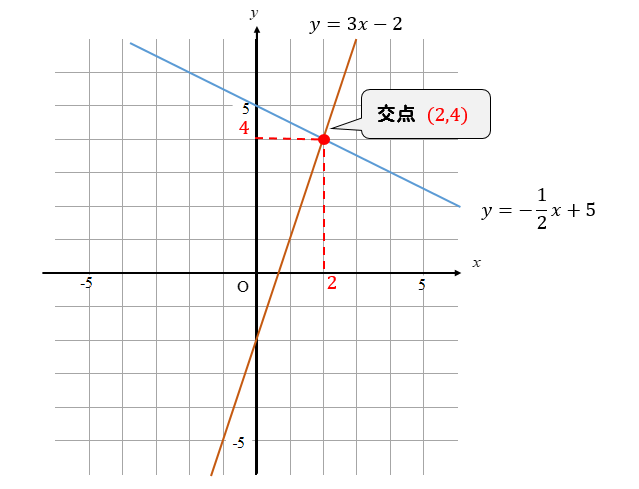



連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト




1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張




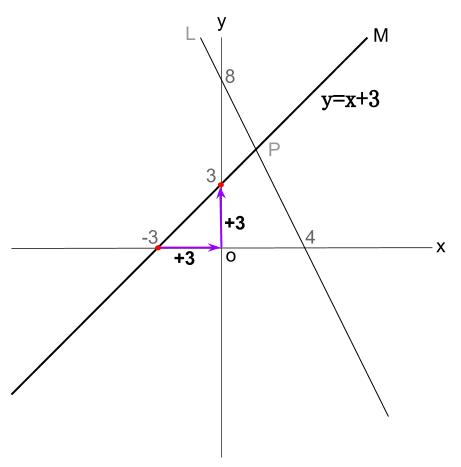
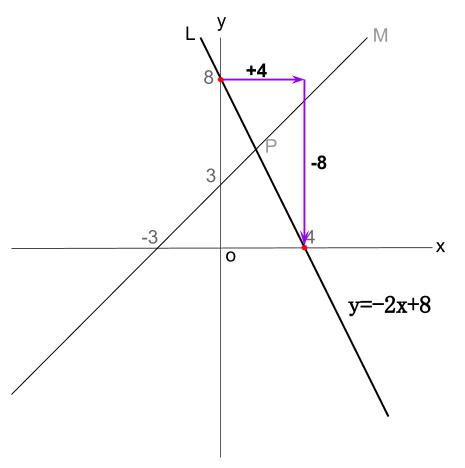
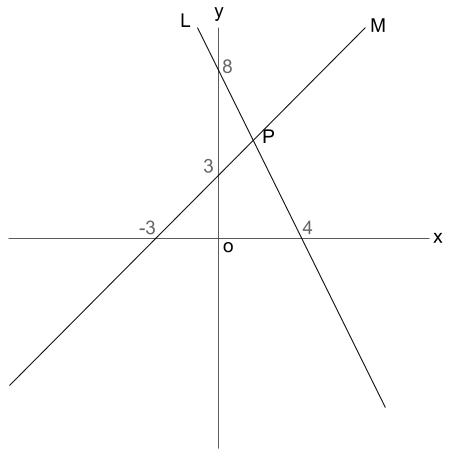
解き方と答えを教えて下さい 次の2直線 L M の交点の座標を Clear



2



0 件のコメント:
コメントを投稿