無料ダウンロード 三 平方 の 定理 二等辺三角形 140222

 三平方の定理は直角三角形の直角を挟む二辺の関係を示しています。 直角を挟む二辺の長さをa、b、そして斜辺の長さをcとすると、a 2 b 2 = c 2 という関係が成り立ちます。 2 三角形が直角三角形であることを確認します。三平方の定理は直角三角形にのみ当てはまり、定義上、直角三角形 三平方の定理（ピタゴラスの定理） 上のような直角三角形で、次の等式が成り立つ。 \begin{equation} a^2b^2=c^2 \end{equation} 直角三角形の2辺がわかれば、残りの1辺も求まるというもので、紀元前から測量等でも使われてきました。日本では中学3年生（義務教育！）で習います。 長い歴史の中で 三平方の定理（ピタゴラスの定理） 直角三角形において， a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」と等しい。 a, b, c a,b,c a,b,c は直角三角形の3辺の長さで， c c c が斜辺です。

エレガント直角 三角形 の 定理 最高のカラーリングのアイデア

三 平方 の 定理 二等辺三角形

三 平方 の 定理 二等辺三角形- 今、二等辺三角形が熱い！ ～小学校の算数が懐かしい デイリーポータルZ 21年5月31日 自分が小学生時代に流行ったマンガやアニメ、おもちゃなどに触れると、懐かしむのみならず改めてハマってしまうことはないだろうか。 筆者は最近、で中学二等辺三角形の面積 例題 ABCの面積を求める。 A B C 13cm 13cm 10cm ABCは二等辺三角形なので,頂点Aから辺BCに 垂線ADを引くとDはBCの中点になる。 A B C 13cm 13cm D 5cm よって、BD=5cm、 ABDで三平方の定理より AD 2 5 2 =13 2 AD 2 = 144 AD>0よりAD=12 面積 =10×12÷2

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

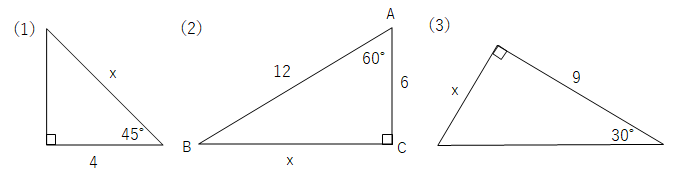
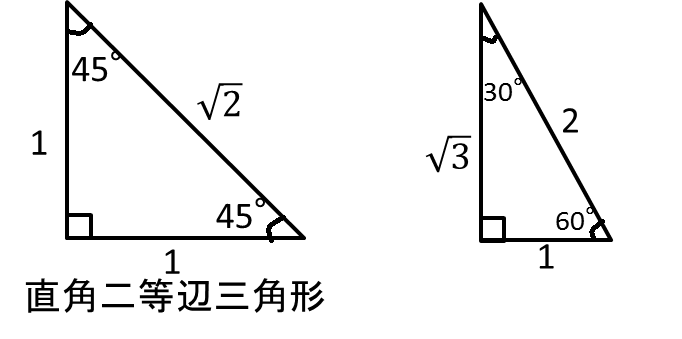
高校受験対策bot 数学 三平方の定理 三平方の定理を習ったら 合わせて覚えておこう 三角定規 90 45 45 1 1 2 直角二等辺三角形 90 60 30 1 2 3 2が斜辺 T Co Rrmbv3lvbw For more information and source, see on this link https//twittercom/juken_taisaku/status/A 2 b 2 =c 2 が成り立ちます．（これを 三平方の定理 といいます．） これを用いて3辺の長さのうち2辺の長さが分かっているとき，残りの1辺の長さを求めることができます． 証明 ・・・ 証明の仕方は何十通り～何百通りあると言われています。 中でも簡単そうなのは次の証明です。 《問題1》 次の直角三角形において，xの長さを求めなさい (1)すると四角形cabo'が長方形になる。 oo'に線を引くと直角三角形coo'ができるので この直角三角形で三平方の定理を使う。 oo'=17, ac=bo'=5, oa=3, つまりoc=8 よってco' 2 8 2 =17 2 計算するとco'=15 co'=abなので ab=15 a b o o' c

② 二等辺三角形・正三角形の理解 ③ コンパス・定規を使っての二等辺三角形・正三角形のかき方 2年生の三角形の勉強は直角のところをみていましたが、3年の三角形の勉強は、辺の長さを特にみていきます。 教え方1 いろいろな三角形をみて、辺の長さに気づかせながら、下の図のように三辺の長さから三角形の種類（二等辺三角形，直角三角形など）を求めるためには， (1) 「AB＝BC」 ならば 「AB＝BCの二等辺三角形」などと答えます． （単に「二等辺三角形」と答えると，BC＝CAの場合やCA＝ABの場合があるので，どの2辺が等しいかを「AB＝BCの」という形で明示することが大切Ama04 練習問題へ abdu は直角二等辺三角形，u bcd は30 °，60 °の角をもつ直角三角形であるから，3 辺 のうちの1 辺の長さがわかると残りの辺の長さも求められる。 ここでは，共通のbd の長さを 調べると，xの値が求められる。 abhu とu ach に分けて，それぞれがどのような辺の比をもつ

三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題とGc_三角中点htm gc_中点連結htm gc_三角形の分割線htm gc_三角形の分割線htm gc_外角の和htm;定理7：三つの辺がそれぞれ等しい二つの球面三 角形は、合同であるかまたは対称である。 球面三角形の2辺が等しいとき、これを二等辺 球面三角形といい、3辺が等しいときは等辺球 面三角形といいます。 これに対して、3辺がすべて異なるとき、これ を不等辺球面三角形といいます。 不

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

1

 Pythagorean theorem は直角三角形の3辺の長さの関係を表す 斜辺の長さを c 他の2辺の長さを a b とすると定理は が成り立つという等式の形で述べられる 三平方の定理さんへいほうのていり勾股弦の定理こう 三平方の定理は、直角三角形の斜辺の2乗が他の辺の2乗の和に等しい、という公式です。 非常に便利ですが、二次方程式になってしまうので解答するのに時間がかかります。 そこで、テストによく出てくる直角三角形については暗記してしまいましょう。 ここでは、特に重要な7つのパ 最短距離と三平方の定理 LINE@始めました。 友達追加をよろしくお願い申し上げます。 勉強のやり方の相談・問題の解説随時募集しています！ お気軽にLINEしてください。 図 1 1 は AB = BC = 6cm,∠ABC = 90° A B = B C = 6 c m, ∠ A B C = 90 ° の直角二等辺三角形 ABC A

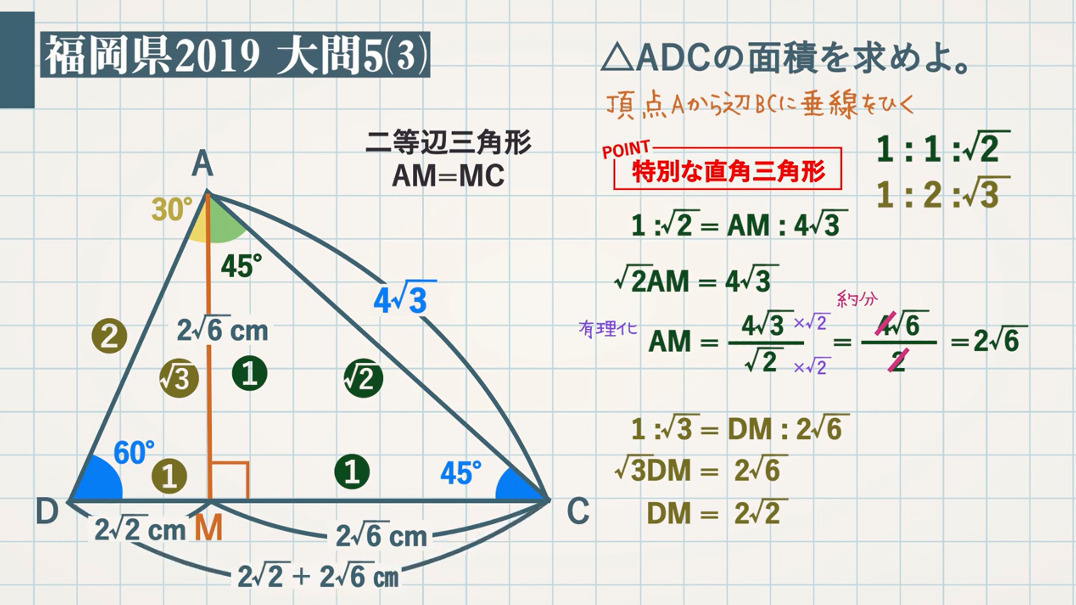
円周角 相似 三平方 特別な直角三角形の比を使い面積を求める 教遊者

エレガント直角 三角形 の 定理 最高のカラーリングのアイデア

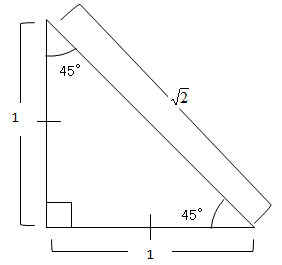
Gc_四角三等分点htm gc_kotaroの定理htm gc_平方 向かい和htm gc 三 平方 の 定理 直角 三角形45°：45°：90°の直角三角形 こちらは直角以外の2角が2つとも45°になっている三角形、すなわち直角二等辺三角形です。これは辺の比が1：1：√2になります。 この三角形の角度と辺の比も必ず覚えておくようにしましょう。 三平方の定理の計算問題の解き方下の図の二等辺三角形の2つの底角は等しいです。 よって、$\angle C$ の大きさも $50^{\circ}$ です。 よって、$\angle B \angle C=100^{\circ}$ です。 三角形の内角の和は $180^{\circ}$ なので、$\angle A$ の大きさは、 $180^{\circ}100^{\circ}=80^{\circ}$ となります。 このように、底角が分かっているときは、 180°から底角の2倍

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

そこで平方の和を作れば, a^{2}b^{2}=cecf=c(ef)=c^{2} (2) を得る以上 3 和算の図形の名称 和算では,均整度の高い図形には特別な名称を与える二等辺直角三角形は 「方」 (正 方形) の半分で 「半方」,二等辺三角形は宝石の形をした 「圭」,直角を挟む二辺が異なる 94直角二等辺三角形ならば一目瞭然ですね！ a 2 b 2 =c 2 逆に、直角三角形ではない 正三角形は一目瞭然でOUT！ ですね a 2 =b 2 =c 2 になってしまいますね それでは、どのような直角三角形でも成り立つという証明に移りますねGc_二等辺三角形の変形htm gc_等辺三角形の変形htm gc_角形htm gc_けいhtm gc_角中点htm;

頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo

応用力 二等辺三角形の面積 小学生対応 2

二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /1 章 図形と相似 1 相似な図形 5 図形の相似/相似な図形の性質・相似比 /三角形の相似条件/相似な三角形と辺 の比/三角形の

15 75 90 の三角形を考える 数学i フリー教材開発コミュニティ Ftext

3

初等幾何学 における ピタゴラスの定理 （ピタゴラスのていり、 英 Pythagorean theorem ）は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} が成り立つという 等式 の形で述べられる 。 三平方の定理 （さんへいほうのていり）、 勾股弦の定理 （こうこげんのていり 二等辺三角形の高さの求め方 まとめ 二等辺三角形の高さを求めるためには まず、頂角からまっすぐな線を引きましょう！ すると、直角三角形を作ることができるので そこから三平方の定理を使ったり 角度がわかる場合には比を取って 高さを求めてき二等辺三角形の性質・定理 二等辺三角形には、 2 つの定理（性質）があります。 ① 2 つの底角の大きさが等しい ② 頂角の二等分線は底辺の垂直二等分線になる これらの定理（性質）を利用して解く問題も多数あるため、とても重要です。 数学質問 直角二等辺三角形と三平方の定理 Duration 1525 イマチュウ塾 2,028 views 1525 二等辺三角形の性質 Duration 500

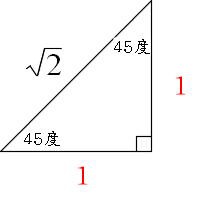
Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

スタディピア 図形

 スチュワートの定理： 三角形 A B C ABC A BC と辺 B C BC BC 上の点 P P P に対して， b 2 ⋅ B P c 2 ⋅ C P = a (B P ⋅ C P A P 2) b^2\cdot BPc^2\cdot CP\\=a(BP\cdot CPAP^2) b 2 ⋅ BP c 2 ⋅ CP = a (BP ⋅ CP A P 2)中学数学（三平方の定理）：直角二等辺三角形 対象 高校生 再生時間 327 説明文・要約 ※ よく出てくる特別な三角形なので、 30°・60°・90°の直角三角形 と併せて覚えておいてください ・直角二等辺三角形（45°・45°・90°）の辺の長さの比 三角形abhだね。 こいつは、 直角三角形2辺の長さがわかってるね。 ってことは、 高さahは三平方の定理をつかえば求められる。 三平方の定理より、 ah = √5^2 – 4^2 = 3 になるね。 おめでとう！ これで二等辺三角形の高さを求められたね！

高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

身近な三平方の定理といえば、小学校からよく使う2つの三角定規です。 直角二等辺三角形の定規の辺の比は、11 √2（内角は、90°、45°、45°） この場合、斜辺が√2です。 1² ＋ 1² =√2²・平面図形のなかに，三 平方の定理を利用する ための直角三角形を見 いだすことができる． ・空間図形のなかに，三 平方の定理を利用する ための直角三角形を見 いだすことができる． ・三平方の定理やこれま でに学んだ図形の性質 を利用して，問題を解 決することができる． ・三平方の 二等辺三角形の定理・性質 二等辺三角形には、\(2\) つの定理（性質）があります。 定理①角度の性質 二等辺三角形の \(2\) つの底角は等しくなります。

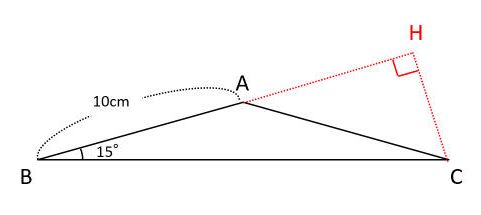
二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

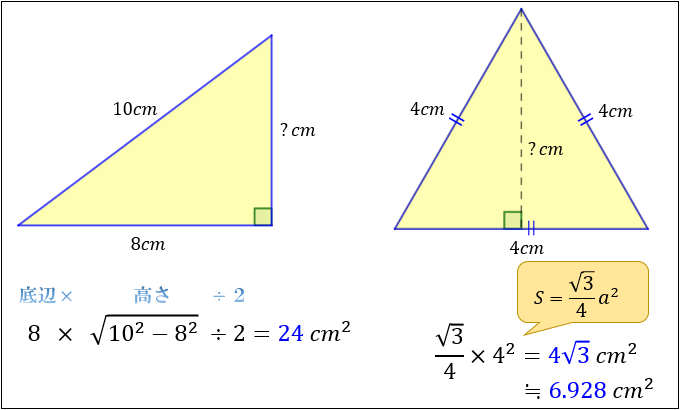
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

三平方の定理の公式で 直角二等辺三角形は１ １ ﾙｰﾄ２という Yahoo 知恵袋

中学三年生です 三平方の定理と相似などで解くそうです ｘを求めてください Clear

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube

テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

三平方の定理 特別な直角三角形 1 ネット塾

二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト

三角比 30 45 60 もう一度やり直しの算数 数学

二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題

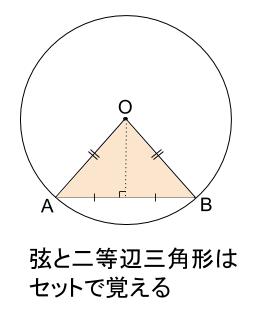
中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

三平方の定理の問題です 図の二等辺三角形abcの高さahと面 Yahoo 知恵袋

1

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

1

直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう

二等辺三角形の斜辺の長さを求めよ 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

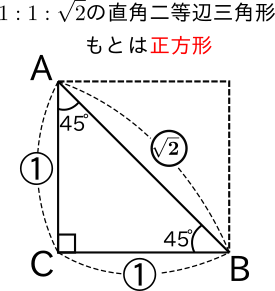
受験数学 三平方の定理で1 1 ルート2は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール

三平方の定理と二等辺三角形 Youtube

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

直角三角形の合同条件とその証明 数学fun

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

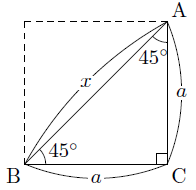
三角定規の3辺の比 まなびの学園

3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

Catatan Tentang 中３ 三平方の定理 台形や二等辺三角形の高さ Clear

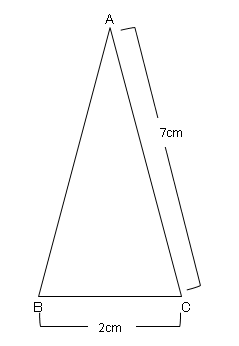
三平方の定理の応用 2 ネット塾

二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

数学 中3 61 三平方の定理 基本編 Youtube

三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも

15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三平方の定理の問題です 直角二等辺三角形の辺の長さを出す問題です わか Yahoo 知恵袋

中3数学 三平方の定理 二等辺三角形の面積 Youtube

三平方の定理と二等辺三角形 Youtube

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

才塾 定期テスト対策

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

Mathematics 三平方の定理 ３ いろいろな三角形 働きアリ

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

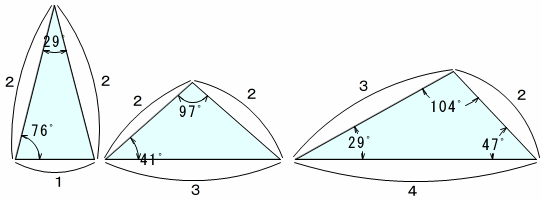
３ ４ ５の三角形で 本当に直角ができる Note Board

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

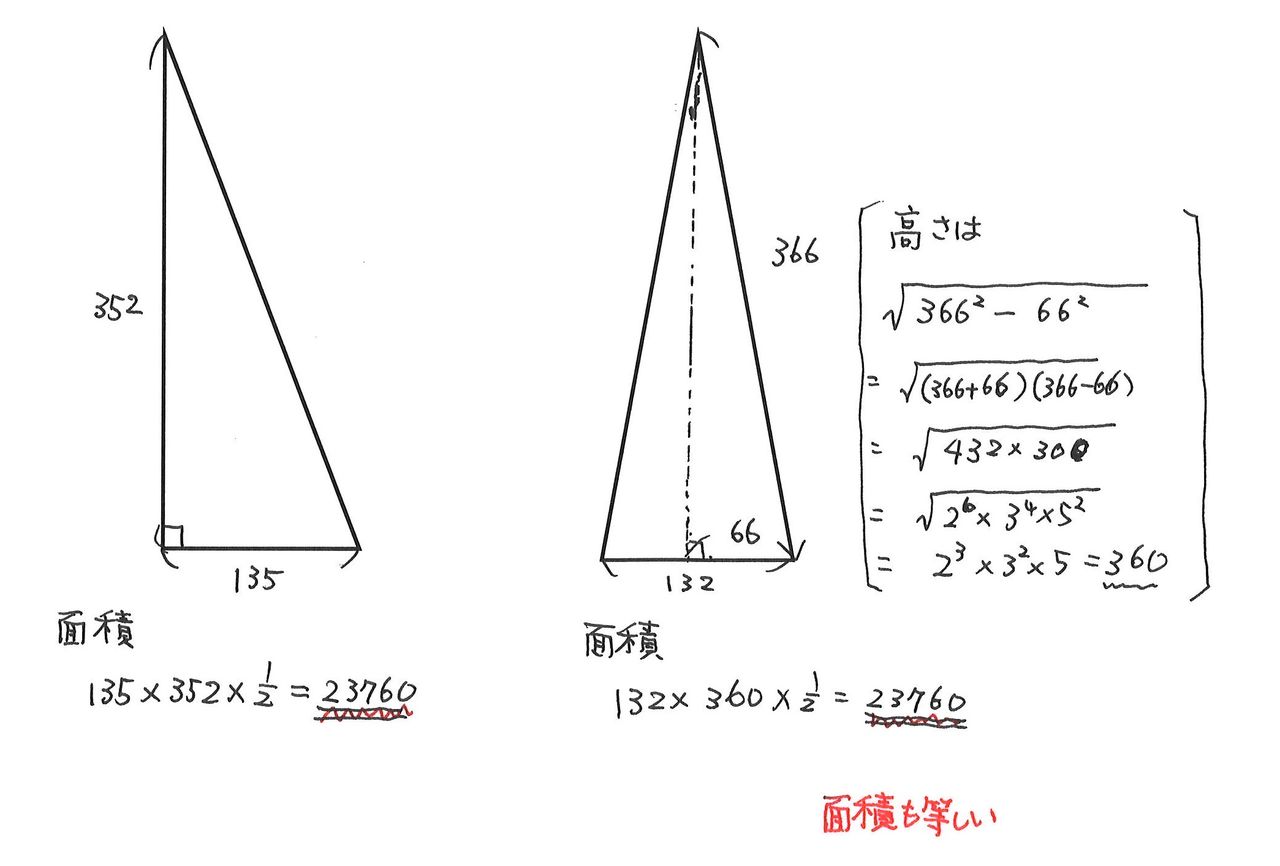
三角形のペア 大田 桐光本部校 ブログ

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく

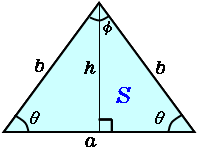
二等辺三角形 高精度計算サイト

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理 おやじさん ネット

中3数学 三平方の定理の定期テスト対策問題 Examee

2

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

2

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

特別な直角三角形の辺の比 無料で使える中学学習プリント

富喜丸くん日記 ３年生数学 三平方の定理の利用

数学 中2 64 二等辺三角形 Youtube

二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

Ohasana Ohasanas Twitter

Tan75 を求める問題の回答と解説です Clear

三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

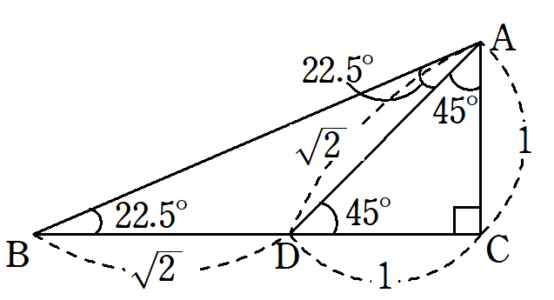
22 5 の三角比 Fukusukeの数学めも

三平方の定理を使うのか 比の計算をするのか 見極め方がよくわかりません Clear

Studydoctor二等辺三角形や台形の面積と三平方の定理 中学３年数学 Studydoctor

受験数学 三平方の定理で1 1 ルート2は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

Clear 勉強ノートまとめアプリ こんばんは 今日は友達とuberしようと思ったらドライバーさんみんな出払ってました 雪だからかな 今日紹介するのは 確認 三平方の定理 直角 二等辺三角形 スクールieさんのノート 大事なところだから

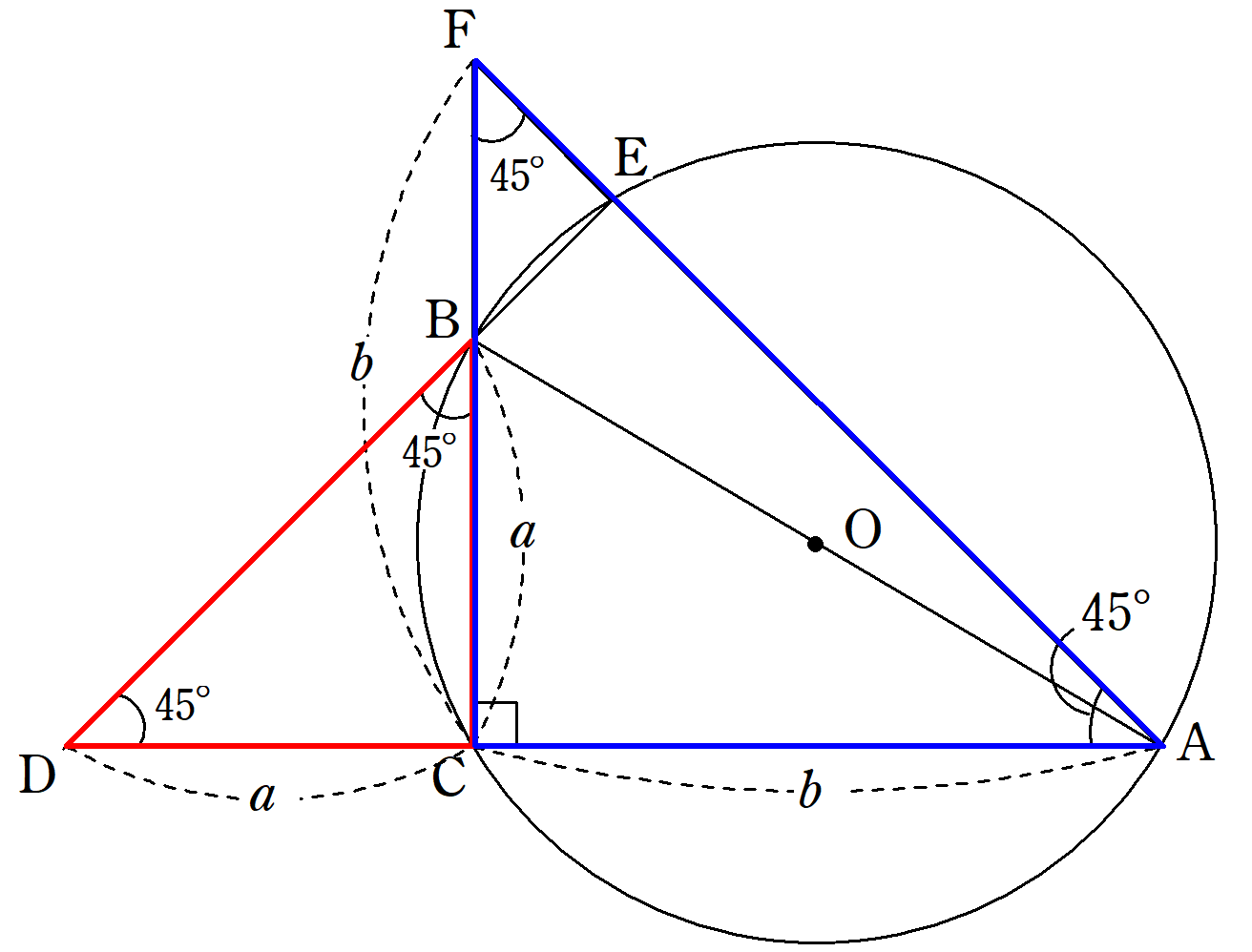
三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも

直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典

高校入試 英語 数学 特別な直角三角形

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

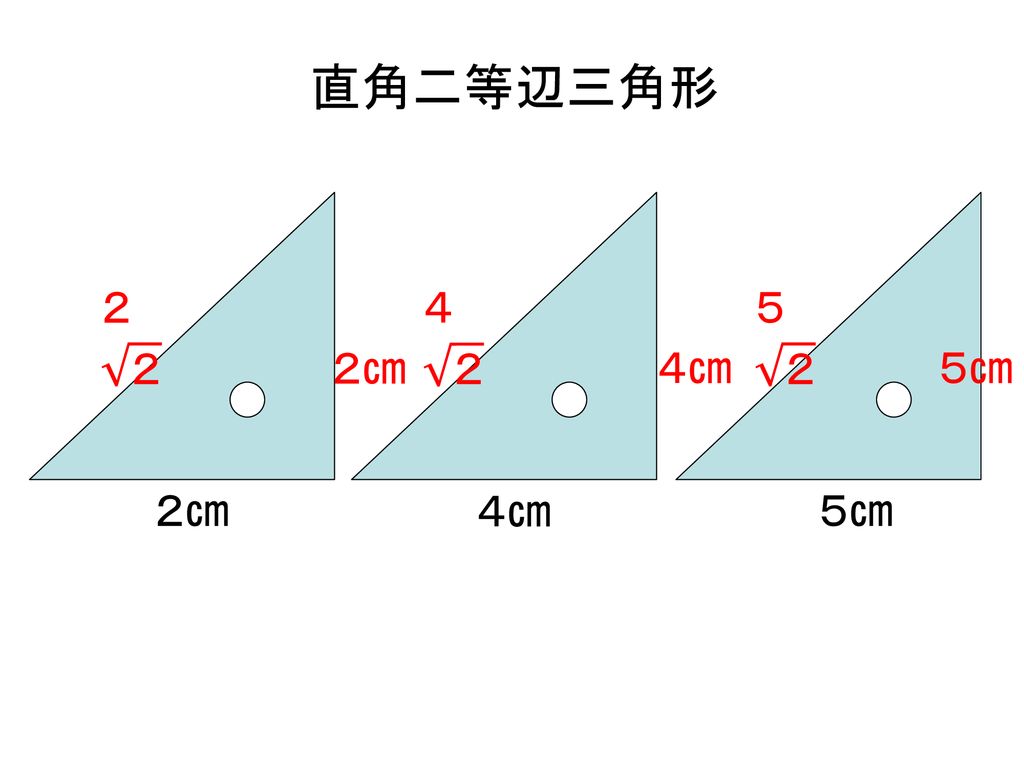
中３数 三平方の定理の利用 内 容 2つの三角定規の3辺の比 平面図形への利用 座標平面上の2点間の距離を求める Ppt Download

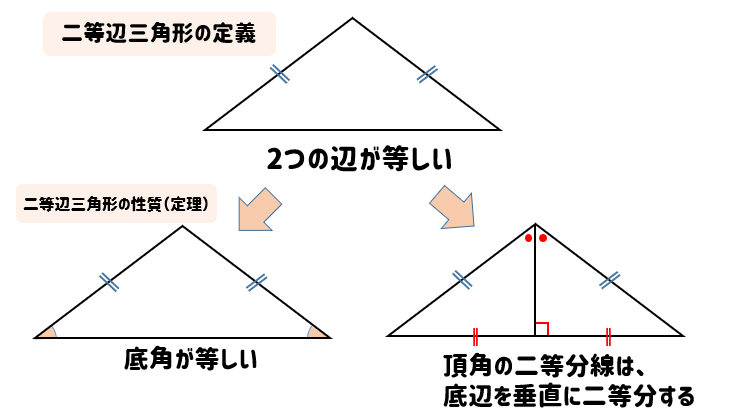
二等辺三角形の定義と性質をサクッと確認しておこう 数スタ

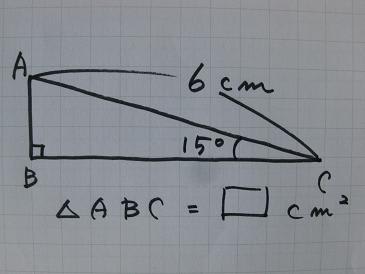
マッキーの教室 中２生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記

三平方の定理の練習問題10問 解き方の解説 数学fun

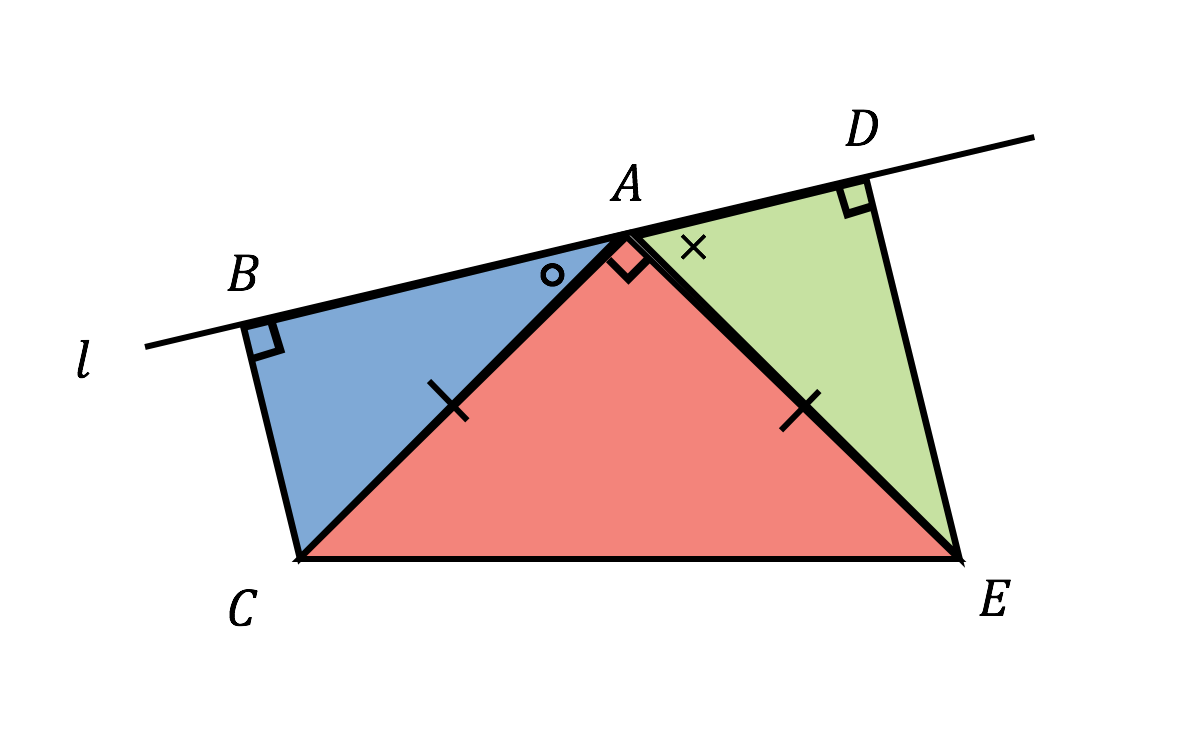
3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく