二 等辺 三角形 三平方の定理 111498-二等辺三角形 三平方の定理

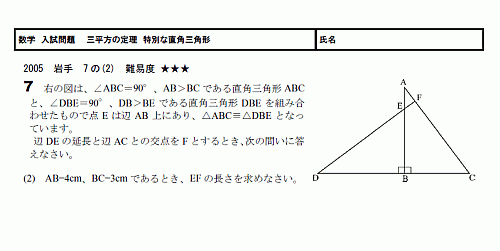
二等辺三角形や台形の面積と三平方の定理中学3年数学 ＜問題＞ ＜答えと解説授業動画＞ 答え （1）2√5 （2）18このため辺の長さがわかっている二等辺三角形の高さを出すことができる。 例AB=AC=3cm, BC=2cmの二等辺三角形の高さを求める。 3cm 3cm 2cm 1cm x やり方 頂点Aから垂線をおろして直角三角形をつくる。 三平方の定理に当てはめる。 x 2 1 2 =3 2 x 2 =91 x 2 =8 x=±2 2 x>0よりx=2 22 特殊な形の三角形で利用される三平方の定理 21 直角二等辺三角形：角度が45°の直角三角形;

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ

二等辺三角形 三平方の定理

二等辺三角形 三平方の定理-三平方の定理 （ さんへいほうのていり ） 、 勾股弦の定理 （ こうこげんのていり ） とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。数学37章三平方の定理「三平方の定理の利用」＜応用問題＞ 組 番 名前 1右の図のように，関数 のグラフ 上に点P，χ軸上に点Q(10，0)があります。 POQがOP＝OQの二等辺三角形に なるとき，点Pの座標を求めなさい。ただし，

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

 高さahは三平方の定理をつかえば求められる。 三平方の定理より、 ah = √5^2 – 4^2 = 3 になるね。 おめでとう！ これで二等辺三角形の高さを求められたね！ まとめ：二等辺三角形の高さの求め方は三平方の定理で1発！ 二等辺三角形の高さを求めたいときは、 頂角の二等分線をひく角b＝50° っていうスペックをもっているヤツさ。 このとき、 二等辺三角形の底角は等しいから、 角b = 角c = 50°になるんだ。 頂角はどうなるかっていうと、三角形は半方 (二等辺) とは異なる図形と考えて 「勾股弦」,そして,各辺の長さがそれ ぞれ異なる (論,三つの角度が異なる) 一般の三角形は 「三角」と呼ばれる拙著 9 643‐635頁を参照 半方 ① 4 山形平 勾股弦\leftrightarrow 角 勾股弦が直角三角形の三辺の関係を表す 《基本定理》 であるのに

三平方の定理1 AMC01 次の図のxの値を求めなさい。 次のような3 辺をもつ三角形のうち，直角三角形であるものをすべて選びなさい。 ① 2 cm， 3 cm，4 cm ② ，32cm，33cm ③ 5cm，25cm，5cm ④ 3cm，2 cm， 5cm 次の図のxの値を求めなさい。 例題1 例題2 例題3 5 AD B C x 6 10 x A B H C 5 三平方の定理にはたくさんの証明方法があります。今回は外接円と直角二等辺三角形を利用した証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理（ピ日本大百科全書(ニッポニカ) 三平方の定理の用語解説 直角三角形abcが与えられたとき、斜辺bcを1辺とする正方形の面積は、他の2辺ab、acを1辺とする二つの正方形の面積の和に等しい。すなわち、 bc2＝ab2＋ac2が成立する。これを三平方の定理という。

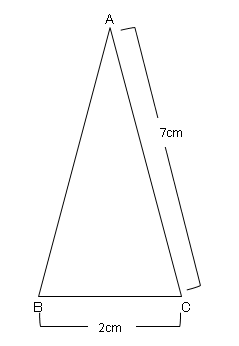
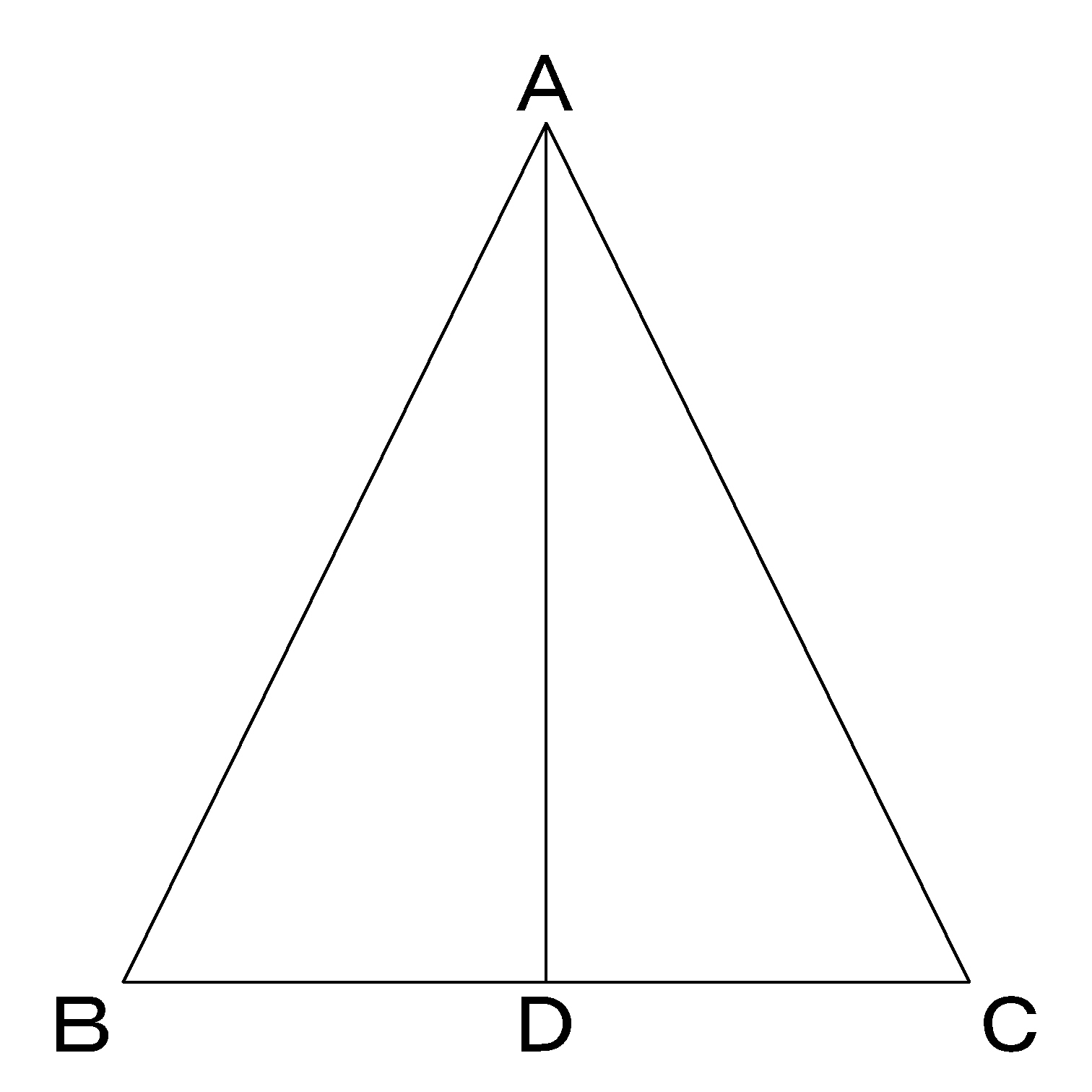
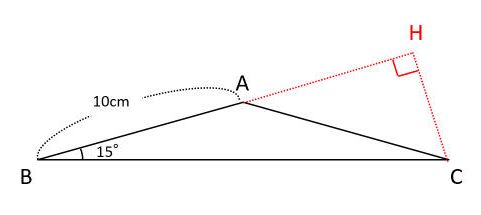
直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) x=2 例2 長方形の向かい合う辺の長さは等しいので，次の図で AH=DC になる． この AH の長さと AB の長さから三角形 ABH について三平方の定理を使うと辺 BH が求まり， HC三平方の定理（ピタゴラスの定理） 直角三角形において， a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」と等しい。28/8/21 二等辺三角形の証明のまとめ ・（証明以外で）二等辺三角形がある時 底角が等しいことを使う 頂角の二等分線を引く→底辺を垂直に二等分する 90°ができる 底辺との交点が、底辺の中点となる ・二等辺三角形の証明 合同な三角形でなく角を利用

三平方の定理 スタディーx

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

9/7/13 三平方の定理より、 AC^2 = 28^2 44^2 AC = 522 cm 円Oの中心点Oを使って三角形ABCを3分割する。 三角形ABC = 三角形OAB 三角形OBC 三角形OCA 円Oの半径をxとして、三角形の面積の公式に当てはめる。 44*28/2 = 28x/2 44x/2 522x/2 616 = 621x x = 99cm 円周を求める 99 * 2 * 31419/2/21 直角二等辺三角形の辺の長さの比 直角二等辺三角形の辺の比は、必ず「 \color {red} {1 1 \sqrt {2}} 」 となります。 1 辺の長さからほかの辺の長さを簡単に求められるので、この比は必ず覚えておきましょう。 なぜこの比が成り立つかは、 三平方の定理 から示すことができます。 三平方の定理 直角三角形の直角を挟む 2 辺の長さを a, b とし、斜辺を c と二等辺三角形の面積 例題 ABCの面積を求める。 A B C 13cm 13cm 10cm ABCは二等辺三角形なので,頂点Aから辺BCに 垂線ADを引くとDはBCの中点になる。 A B C 13cm 13cm D 5cm よって、BD=5cm、 ABDで三平方の定理より AD 2 5 2 =13 2 AD 2 = 144 AD>0よりAD=12 面積 =10×12÷2

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

直角三角形の合同条件 数学が嫌いなんです

あとは、三平方の定理で解決します。 ここで、計算を簡単にするために、 y = 1 y = 1 のときの相似な三角形で長さを求めましょう。 三角形 AEH A E H に三平方の定理を使うと、 AE = √10 A E = 10 なので、 これは、本来の図と相似比が 8 √10 8 10 です。 三角形○ 01 三平方の定理とは 直角三角形の直角を挟んだ2辺の長さをaとb、直角に対する斜辺 (もっとも長い辺)の長さをcとすると (図Math001)、つぎの等式が成立ちます。7/3/15 です。これは直角二等辺三角形の場合の三平方の定理ですね！ やはり、ピタゴラスは只者ではありません。 ちなみに、上のタイルを一般の直角三角形に応用した図は です。ここで面積が 大きな正方形＝小さな正方形＋直角三角形×4

三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ

U9j580gf8iba369ji2w Xyz P 11

直角二等辺三角形 C言語で図形の面積を求めるプログラムの参考にさせていただきました。 計算式が書いてあるのが親切でいいと思いました。 私もあずま袋を縫いたくて計算しました。 やっぱり50×150がベストっぽい！ 小鳥が餌を食べる為の囲いを作る30/1/ 三平方の定理 （基礎） 三角定規 三角形の いろいろな長さ 二等辺三角形の面積 三平方の定理 (四角形の対角線) 三平方の定理 (図形の面積) 三平方の定理 (直方体の対角線) 三平方の定理 (2点間の距離) 三平方の定理 (円すい・角すいの体積)11/3/ 二等辺三角形の定理・性質 二等辺三角形には、\(2\) つの定理（性質）があります。 定理①角度の性質 二等辺三角形の \(2\) つの底角は等しくなります。

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

Tan75 を求める問題の回答と解説です Clear

二等辺三角形と定理・定義 ab＝acの二等辺三角形で、bd＝ceとすれば、∠ade＝∠aedであることを証明しなさい。という問題で、 abdと aceの合同を示し、対応する辺が等しいことからad＝ae。 adeは二等辺三角形だから 三平方の定理の公式で、直角二等辺三角形は1三平方の定理1 AMA01 1 三平方の定理 ここでは，直角三角形の辺の長さの関係について学習してみましょう。 A三平方の定理（ピタゴラスの定理） 直角三角形の直角をはさむ2 辺の長さをa，bとし，斜辺の 長さをcとすると a2 ＋b2 ＝c2 が成り立つ。もくじ 1 三平方の定理の内容：直角三角形と辺の長さの関係 11 分からない辺の長さを計算できる三平方の定理;

三平方の定理で15 75 90のとき 6 2 6 2 4という直角 Yahoo 知恵袋

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ 二等辺三角形では底角の大きさが等しい んだ。 たとえば、つぎの二等辺三角形abcがあったとしよう。 ab = ac;△ABFで三平方の定理を使うと (10−x) 2 =6 2 x 2 100−xx 2 = 36x 2 −x=36−100

三平方の定理の応用 2 ネット塾

三平方の定理 おやじさん ネット

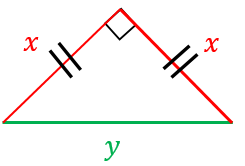
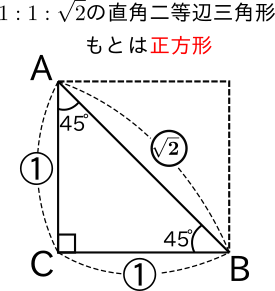
中学数学（三平方の定理）：直角二等辺三角形 対象 高校生 再生時間 327 説明文・要約 ※ よく出てくる特別な三角形なので、 30°・60°・90°の直角三角形 と併せて覚えておいてください ・直角二等辺三角形（45°・45°・90°）の辺の長さの比9/5/17 以上の三角比は三平方の定理でも学習します。 ※三平方の定理を学習したい人は、 三平方の定理について詳しく解説した記事 をご覧ください。 直角二等辺三角形の三角比は辺の長さを求める時に使うので、必ず暗記しましょう！13/6/17 辺の比率 直角三角形の性質を有することから、その辺の比に三平方の定理を適用することができ、結果として、その辺の比にかなりの特殊性が生まれることになります。 つまり、内角がそれぞれ90°、45°、45°の二等辺三角形の三辺の比は、1：1：√2となるのです。 この公式はかなりの頻度で利用する必要が生まれますので、是非とも覚えてしまうことをお

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

4/3/19 まぁ、三平方の定理でも解けますね。 しかし、もし、4ではなく04などの小数や分数が出た場合は、ちょっと計算が苦しくなります。 あくまでも、一時しのぎと考えて使ってください。 本来は、 比を利用するのがベスト です。 Tweet ← 受験数学：三平方7/8/21 その二等分線は、円O1の中心を通り、円O2とO3の接点を通ります。 その二等分線で、この三角形を半分に切りましょう。 下の図が、半分に切った三角形の左側です。 直角三角形となります。 三平方の定理により、3辺の長さは6、8、10となります。22/3/17 直角二等辺三角形の辺の長さの比は 1 1 √2 でしたから、 と分かります。 三平方の定理の応用 三平方の定理が成り立つ整数の組 三平方の定理は、平方が登場してくる関係上どうしてもルートが出てきやすくなってしまいます。

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ

二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

二等辺三角形の高さを\ 三平方の定理の証明｜直感的に分かる図で解説します 三平方の定理は直角三角形の辺の長さに関する定理ですが、今後、図形だけではなく関数などあらゆる分野でも利用することになる重要な定理です。直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) x=2 例2 長方形の向かい合う辺の長さは等しいので，右図で AH=DC になる． この AH の長さと AB の長さから三角形 ABH について三平方の定理を使うと辺 BH が求まり， HC，AD

3点の座標が与えられたとき その三角形はどんな三角形か答える問題 数学の偏差値を上げて合格を目指す

三平方の定理の公式で 直角二等辺三角形は１ １ ﾙｰﾄ２という Yahoo 知恵袋

Wordで使える 二等辺三角形の合同の証明の図 Wordで数学問題プリントを作ろう

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

Clear 勉強ノートまとめアプリ こんばんは 今日は友達とuberしようと思ったらドライバーさんみんな出払ってました 雪だからかな 今日紹介するのは 確認 三平方の定理 直角 二等辺三角形 スクールieさんのノート 大事なところだから

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

1

2

3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

1

頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo

二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト

応用力 二等辺三角形の面積 小学生対応 2

直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

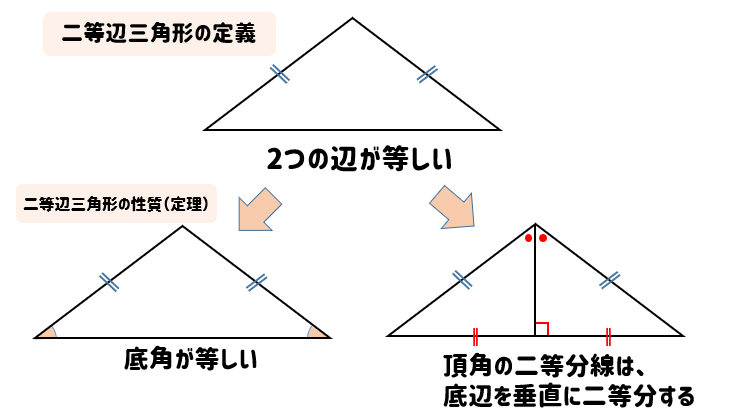
二等辺三角形の定義と性質をサクッと確認しておこう 数スタ

高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月

3

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

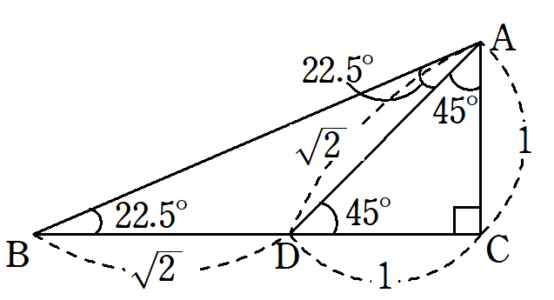
22 5 の三角比 Fukusukeの数学めも

特別な直角三角形の辺の比 無料で使える中学学習プリント

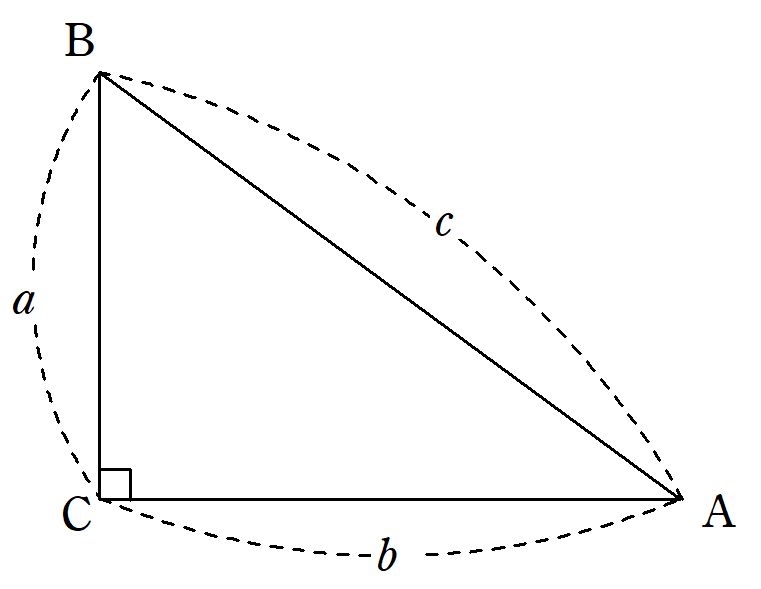
三平方の定理の証明 トレミーの定理による証明 Fukusukeの数学めも

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

受験数学 三平方の定理で1 1 ルート2は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール

世界一わかりやすい数学問題集中３ ７章 三平方の定理

二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

Studydoctor二等辺三角形や台形の面積と三平方の定理 中学３年数学 Studydoctor

2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

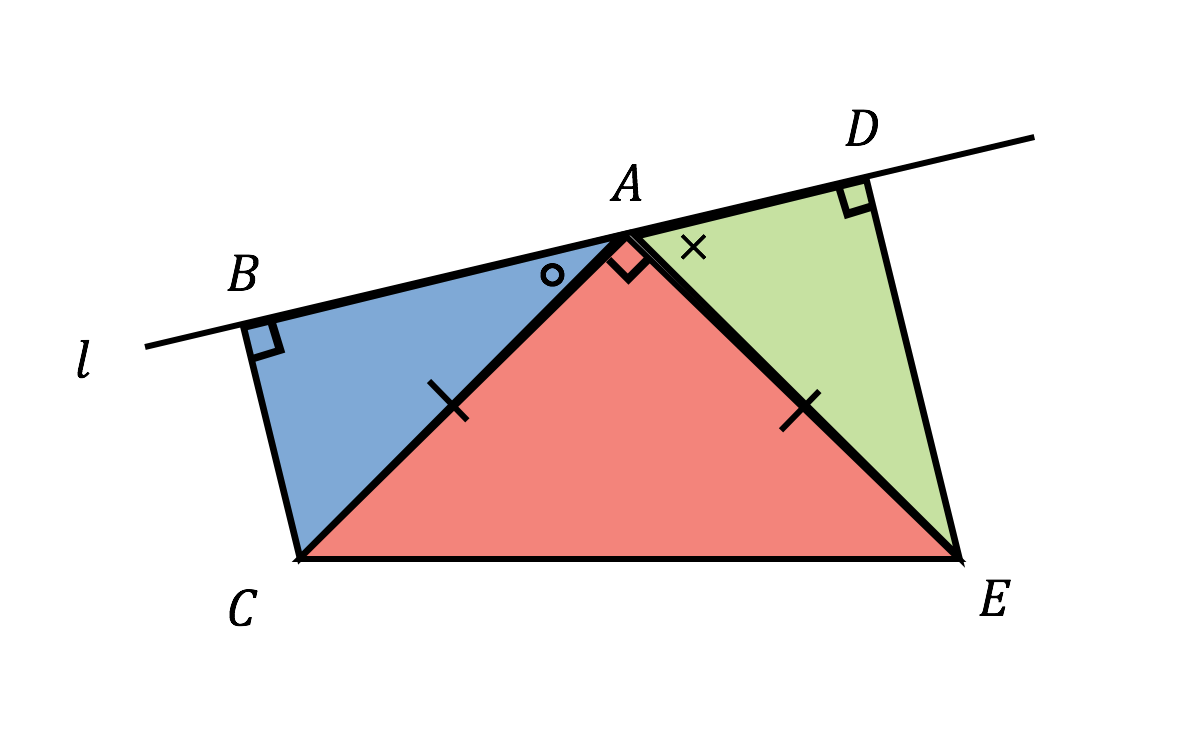
3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく

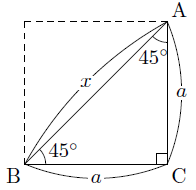
三角定規の3辺の比 まなびの学園

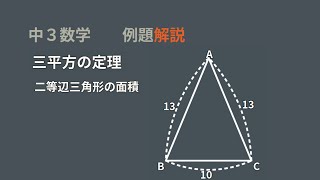
二等辺三角形の面積

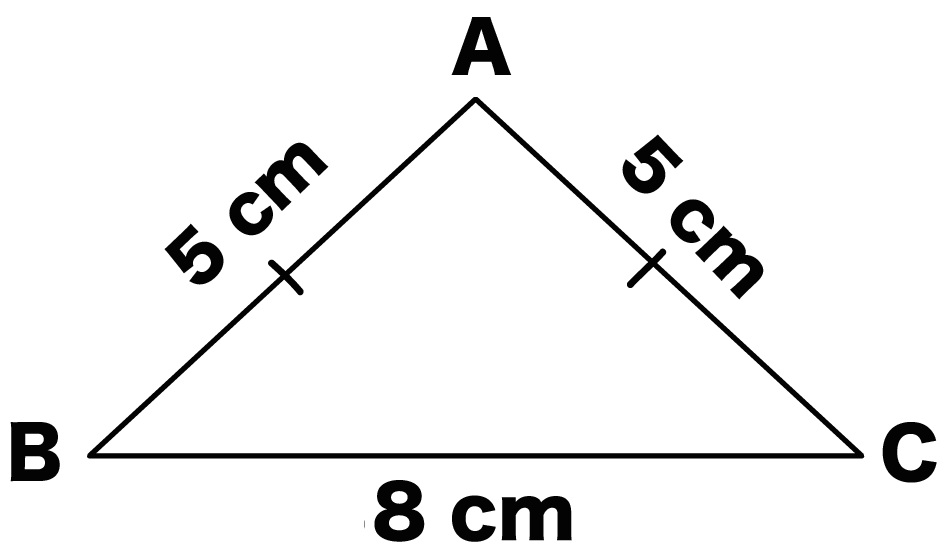
簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

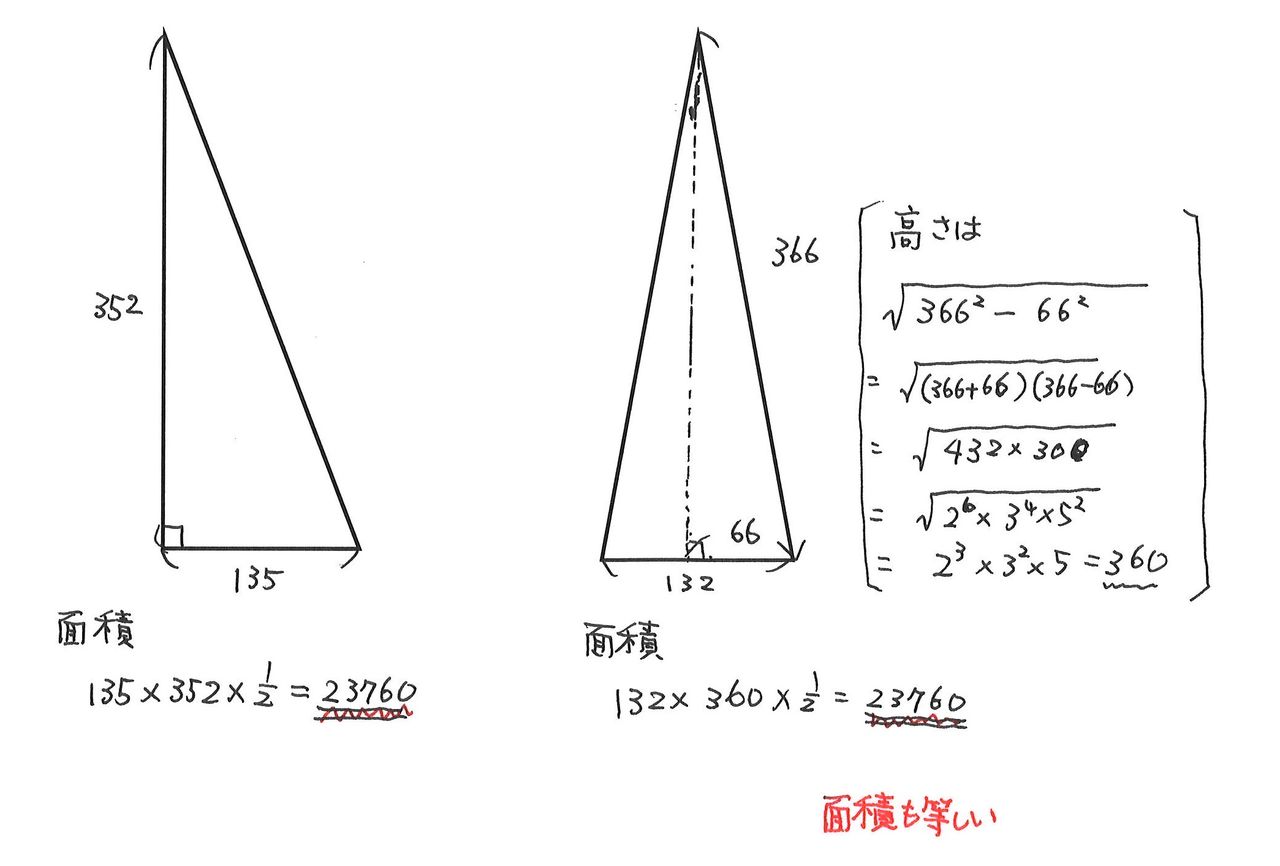
三角形のペア 大田 桐光本部校 ブログ

直角三角形の合同条件とその証明 数学fun

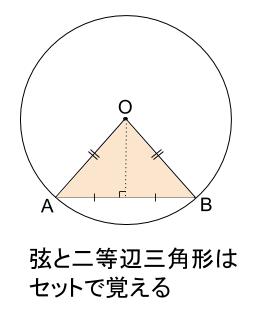
中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角比 30 45 60 もう一度やり直しの算数 数学

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

三平方の定理の二等辺三角形の比がありますが それを使うにはその図形の角度が写真のよう Clear

二等辺三角形の面積を求める算数の公式は

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

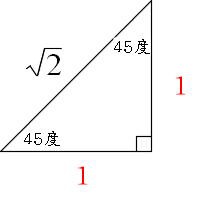
Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

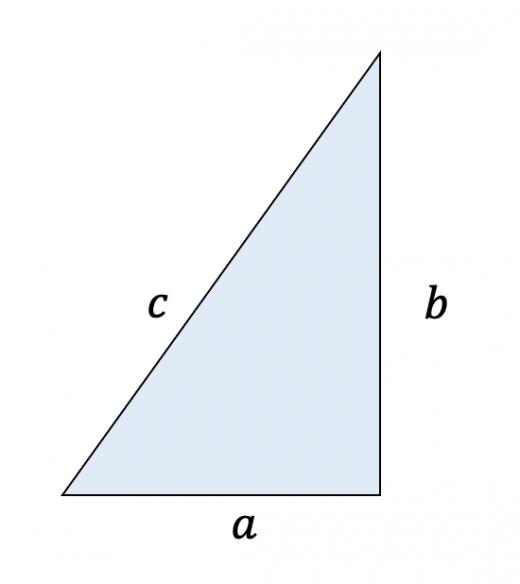
直角三角形の定義とさまざまな公式 高校数学の美しい物語

受験数学 三平方の定理で1 1 ルート2は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール

1

Http Www Edu Tens Net Kyouikuken Basic Takamatsu Pdf Jsanques S9 07 Pdf

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

富喜丸くん日記 ３年生数学 三平方の定理の利用

Mathematics 三平方の定理 ３ いろいろな三角形 働きアリ

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

三平方の定理と二等辺三角形 Youtube

富喜丸くん日記 ３年生数学 三平方の定理の利用

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

直角三角形 Wikipedia

スタディピア 図形

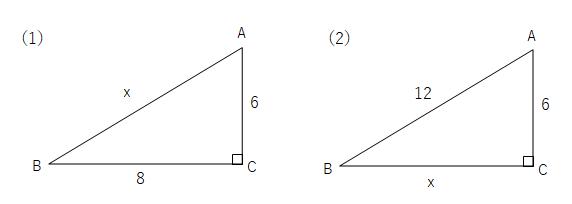
中3数学 三平方の定理の定期テスト対策問題 Examee

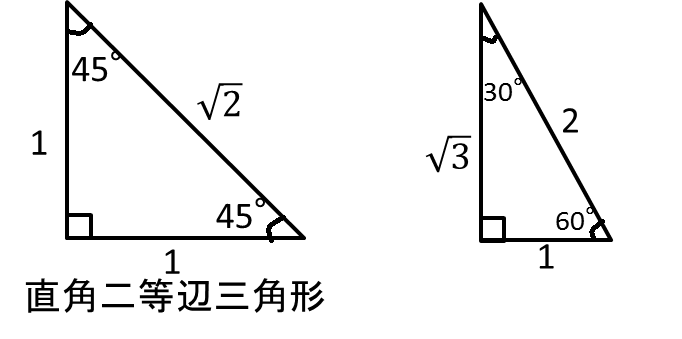
高校受験対策bot 数学 三平方の定理 三平方の定理を習ったら 合わせて覚えておこう 三角定規 90 45 45 1 1 2 直角二等辺三角形 90 60 30 1 2 3 2が斜辺 T Co Rrmbv3ukcw

高校入試対策数学 三平方の定理と関数の融合問題 Pikuu

エレガント直角 三角形 の 定理 最高のカラーリングのアイデア

中学三年生です 三平方の定理と相似などで解くそうです ｘを求めてください Clear

変な証明2

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube

二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典

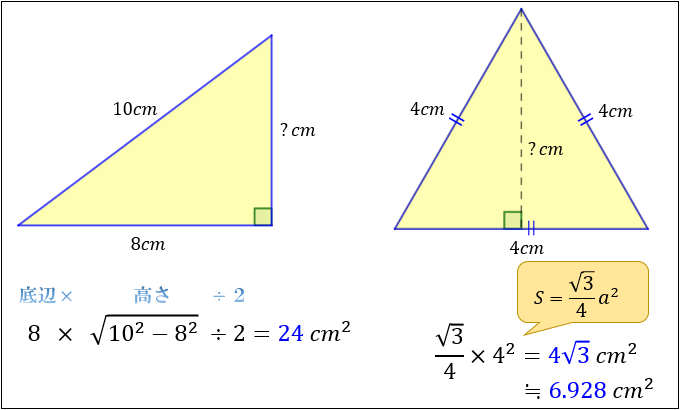
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

15 75 90 の三角形を考える 数学i フリー教材開発コミュニティ Ftext

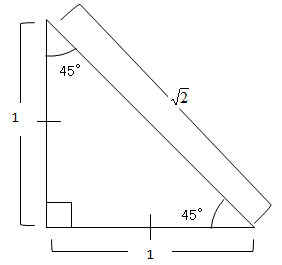
三平方の定理 特別な直角三角形 1 ネット塾

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

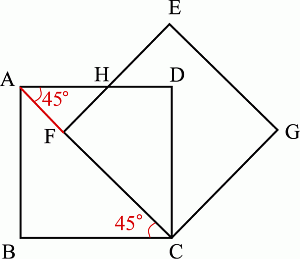
三平方の定理 無料学習プリント教材

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

Incoming Term: 二等辺三角形 三平方の定理,