1011 零点 特異点の場合とは逆に、f(z)のz = z0 におけるローラン展開が正べきの部分しか持たない場合、 z = z0 における関数値はf(z0) = 0となる。このとき、z = z0 は関数f(z)の零点であると呼ぶ。 特に、ローラン展開したときに f(z) = ∑1 n=m an(z z0)n = am(z z0)m am1(z z0)m1 のようにm次の項から級数がルート2が無理数であることの4通りの証明 レベル ★ 入試対策 式の計算 更新日時 2 \sqrt {2} 2 は無理数である。 より一般に,平方数でない正の整数問題 n が1 より大きい奇数のとき、n3 ¡n は24 の倍数であることを示せ。 定理124 (a,c) = 1, d j c ならば(a,d) = 1 証明 仮定と定理122により、au cv = 1 を満たす組(u,v) が存在する。また、 仮定によってc = kd と書けるから、関係式au dkv = 1 と書ける。これはすなわ
Nの2乗を6で割ったときの余は 0か1か3か4であることを証明せよ と Yahoo 知恵袋
一の位が5 2乗 証明
一の位が5 2乗 証明-1のn乗根の導出 一般の n n n に対して冒頭の定理1を証明します。 いくつか考え方はありますが,前提知識として「複素数の積と回転が対応していること」の理解が必要になります。 →複素数平面における回転と極形式 →ド・モアブルの定理の意味と証明 log 10 5 = log 10 (10 / 2) = 1 – log 10 2 = より 10 = 5;




実数の2乗は0以上 の使い方 数学 苦手解決q A 進研ゼミ高校講座
ワンポイント数学3|根号 (ルート)の基本と二重根号の外し方 根号 (ルート)の中身が2乗であれば,根号 が外れるのはよく知られていますが,そこでよくある間違いがあります. 実数 a に対して, a 2 で根号 を外すとどうなるのか,正しく言えるでしょうか 証明しておこう。 証明 ( 10 a 5) 2 = 100 a 2 100 a 25 これを次のように変形するのがポイント。 ( 10 a 5) 2 = 100 a ( a 1) 25 これは a ( a 1) を100倍して25を加える計算だから,下二桁は必ず25になる。 つまり,十の位の数字とそれに1を加えた数字の積を2 1000 の1の位の数を求めなさい。 (答案) 2のn乗の1の位の数は,2→4→8→6のように4個ずつ繰り返し,nが4で割り切れるとき6となる。 2 1000 =2 4×250 だから6・・・答 (別解) 2 4 の1の位の数は6 1の位が6のとき、何乗しても1の位は6 ※1
では,2桁の自然数十の位をa,一の位をbとしてみましょう。2桁の自然数を,aとbを使ってどうやって表せばいいでしょうか。 例えば25だと十の位は2,一の位は5。 25を十の位である2と一の位である5を使ってどう表現するでしょうか? 十の位×一の位?2×5=10この結果から、 zのn乗根n p = R(cos isin) が式(5)の通りに得られる。 2m n ˇの部分を除けば、元の複素数z = r(cos isin )と比べて、絶対値は1=n乗(j n p zj = r1=n)、 偏角は1=n倍(argz = n 2mˇ n)で、ド・モアブルの定理と同じ形になっている。 特に、1のn乗根は(r = j1j = 1 こんにちは、ウチダです。 今日は、計算力を上げるのにもっとも効率的な 「インド式計算(法)」 について、私が感動した計算法の中からオススメ順でご紹介したいと思います! かけ算わり算や19×19までの九九、単純な足し算において効果抜群ですよ♪ (一部証明もご紹介します。
このように,2 0 , 21 の値を考えることができますね。 さらに,表記のしかたを少し変えてみましょう。 と書きかえることができます。つまり,n を正の整数とすると, と表せます。そこで, 「マイナス 乗」のときは,「分数の 乗」にする! 45の2乗(45 x 45)の場合 1の位が5の整数は、"5"を除いたケタの数にその次の数をかけ("4"ならその次の"5"をかける)、下2ケタに25をつけた数が2乗になる。 「45」の場合、5を除いた4に5をかけて4 x 5 = 「」 このの後に下2ケタ25をつけると、答えは「25」に・n が5 の倍数 ⇔ n の一の位の数が0 か5 ・n が4 の倍数 ⇔ n の下2 桁の数が4 の倍数 ・n が3 の倍数 ⇔ n の各位の数の和が3 の倍数 ・n が9 の倍数 ⇔ n の各位の数の和が9 の倍数 解答 (1) 5 個の自然数のうち,一の位の数が偶数であるものは 16,18 (2) 5 個の




この問題の解説をよろしくお願いします Clear




基本対称式について6乗和の値を因数分解公式を使って求める タロウ岩井の数学と英語 Note
インド式2乗(下1桁が5の数) 役に立たない。 インド式計算法は愚者の計算法である。 ほとんどが中学で習う展開公式の応用に過ぎないので展開公式を理解していればほぼ無用。 暗算で解けと言っているが、実際には計算途中の数字は憶えていられない100 ≡ 2 100 ≡ 2 ( mod 7 ( mod 7 ) となります.しかし, 100 100 を 7 7 で割ると 13 13 余り 9 9 と書けなくもないですよね? つまり 100 ≡ 9 100 ≡ 9 ( mod 7 ( mod 7 ) と書いても正しいです.合同式としては 余りが割る数より大きくてもかまいません. なんなら 100 100 をとができる。十の位が a ,一の位が b の2 けたの整数は, 10×a b = 10a b と表すことができる。同様にして,百の位 が a ,十の位が b ,一の位が c である 3 けたの整数は, 100×a10×bc =100a 10b c と表すことができる。 問題(1 学期中間) 3 けたの自然数を,百




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



Nの2乗 1は8の倍数を 証明せよ で 回答は写真のようなのですが Yahoo 知恵袋
112 留数定理 117 注意3:Cauchy の積分定理,Cauchy の積分公式は,この定理の特別な場合である。 Cauchy の積分定理(CauchyGoursat の定理): 区分的になめらかなJordan 曲線C の上と内部でf(z) が正則ならば,曲線C を一周す る積分は0 になる: C f(z)dz =0 Cauchy の積分公式: 区分的になめらかなJordan2の倍数の性質は以下のようになります。 ・2の倍数は一の位だけ見ても2の倍数 (例 4, 8, 36, 152, 600) ・2の倍数にどんな整数をかけても2の倍数 (例 2 × 3 = 6, 16 × 27 = 432 ) また、2の倍数以外の整数を 奇数 と呼びます。 偶数と奇数については、以下のような性質実数指数の累乗の定義 ~ 10進近似列を用いて ・「『正の実数』aの実数r乗」a r は、どのように定義されているのか? 実数rは、有理数であるか、無理数であるかのいずれか。 (i) 実数rが有理数である場合、 a r の定義として、「aの有理数r乗」a r の定義をそのまま使う。




三乗の公式 A B 3乗の展開公式と覚え方を解説




なぜ Aの0乗は1 なのか その納得の理由を紹介します 数学の面白いこと 役に立つことをまとめたサイト
5の倍数 : 一の位が0か5 。 例:1236 5 、8465 0 など 6の倍数 : 偶数かつ3の倍数 。 (2の倍数でもあり3の倍数でもある) つまり、 各位の数の和が3の倍数で、一の位が偶数 である数です。 例: (各位の数の和) さて,上で書いたことが理解できていれば, m > 3 の場合でも,2乗和,3乗和と同様に和の公式が導けることが分かりますね. k m 1 − ( k − 1) m 1 は m 次式ですから,上の方法と同様にして4乗和,5乗和と順に求めることができます. 計算は非常に多く証明 十の位が同じで一の位がたして10になる2桁の掛け算(少し難しい) 72×78=7×(7+1)×100+2×8=5600+16=5616 ②①を100倍する. 56×100=5600 ④②と③をたす. 5600+16=5616 証明 それぞれの数を10a+b,10a+(10-b)とする.




4乗和と5乗和の公式の証明 降階乗利用 怜悧玲瓏 高校数学を天空から俯瞰する
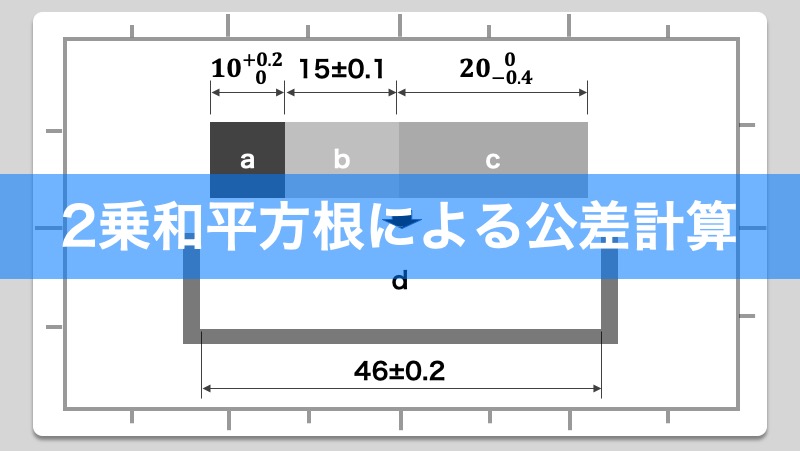



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
千の位は1,3,5,7,9の5通り 一の位は偶数0,2,4,6,8の5通り 百、十の位は残りの8個から2個とった順列 8 p 2 よって5×5× 8 p 2 =5×5×8・7=1400 個 2千の位が偶数の場合 0以外の偶数 偶数 千の位は2,4,6,8の4通り 一の位は千の位で使われた以外の偶数と0なので4通り 合同式(mod)とは? 性質の証明や計算問題の解き方 21年2月19日 この記事では、「合同式 」についてわかりやすく解説していきます。 合同式の性質や解き方、不定方程式との関係なども説明していきますので、ぜひこの記事を通してマスターして1の位の数字が「5」の時の2乗を計算する方法を応用して、 10の位の数字が同じで、1の位の数字の合計が10になる場合にも計算を簡単にすることができます。 3×3|3×5+5×3|5×5 3×3| 3×(5+5)|5×5 3×3| 3×10 |5×5 3×3| 30 | 25




5分でわかる逆2乗の法則 どんな例がある 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン
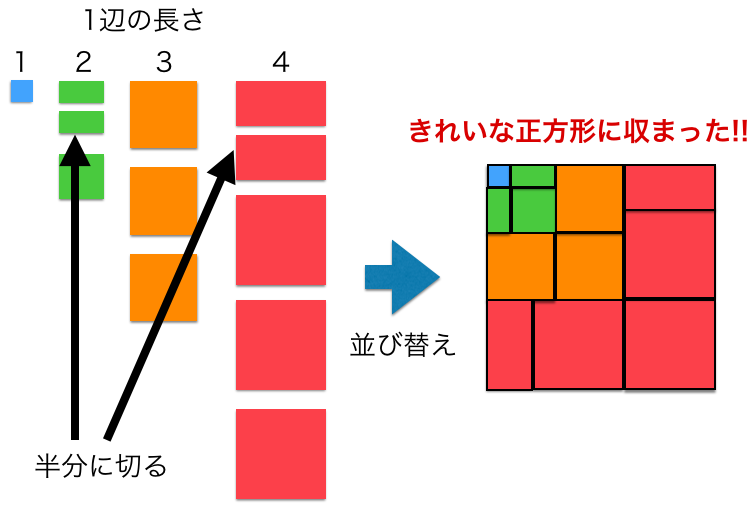



暗記しない数学 3乗和のシグマ公式を図形で理解してみる ロボット It雑食日記
\(\sqrt{2}\)は「ルート2」、\(\sqrt{3}\)は「ルート3」というように読みます。 そして、根号で表す数には 「根号の中はできるだけ簡単な整数の形にする」 というルールがあります。 言いかえれば、「整数の2乗の因数があれば根号の外に出す」ということです。 根号の外に出せる因数は外に出す56の十の位の数は5, 一の位の数は6である。 この5, 6を使って56という数字を表すと 56 = 50 6 = 5×10 6 となる。 つまり (2けたの自然数)=(十の位の数)×10(一の位の数) 一の位の数と十の位の数との和が12となる2けたの自然数がある。Log 10 6 = log 10 2 log 10 3 = より 10 = 6;




1乗和 2乗和 3乗和の公式 導出法から理解しよう




3乗の因数分解 展開 公式 理系ラボ
2分の1乗の意味 2分の1乗ってどういう意味? 1/2乗,1/3 乗がわかりません。 3の1/2乗 はどうやって計算するんですか? 進研ゼミからの回答! こんにちは。 いただいた質問について,さっそく回 一の位が5である数は 10の位をmとおくと (10m+5)^2=25(4m^2+4m+1) =100m(m+1)+25 したがって10の位と10の位に1を加えたものの積に、25を最後に書き加えたのが答えになります たとえば 35^2は3×(3+1)=12 12に25を書き加えたら1225 これが35^2の答えにな下2桁が4で割り切れるか00。 ・ 5で割り切れる数(5の倍数) 1の位が0か5。 ・ 6で割り切れる数(6の倍数) 1の位が偶数、かつ、各位の数の和が3で割り切れる。 ・ 8で割り切れる数(8の倍数) 下3桁が8の倍数か000。
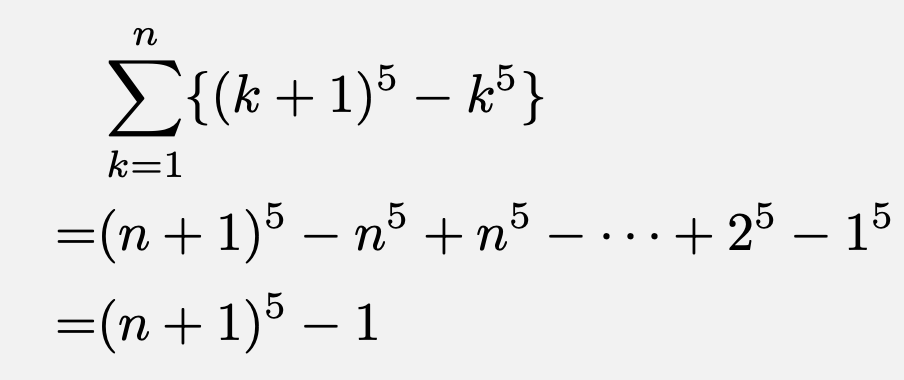



シグマの公式 2乗 3乗 4乗 の証明は 数列の和はこれでマスター 東大医学部生の相談室
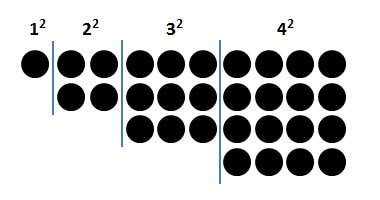



まとめ 2乗の和の公式の求め方 いろいろな方法をご紹介 ここからはじめる高校数学
下1桁が5の自然数の2乗の計算 一の位が5で、十の位が a a の自然数の2乗は、 下2桁が25、さらに百の位が a(a1) a (a 1) となる。証明がついてないものはLittlewoodRicahrdson ruleなどです(その証明は2を 参照.このノートを読んだあとなら難しくないと思う). シューア多項式などの対称式は,いろんなところでお見かけする重要な話題で,このことから 10 < 10 0746 < 10 となりますので、問題の 12 60 の最高位の数字は 5 であることがわかりました。最高位以外の数字は残念な




1の3乗根 オメガ W をなるべくわかりやすく解説してみる 高校数学の知識庫



1
有理数指数の累乗の定義 z, n を「 q = z / n 」を満たす整数, 自然数 の組としたときの、 az/n のこと。 この整数 z, 自然数 n の取り方に依存せず、 aq は同一の 実数 となる → 定理 。 上記の定義を az/n の定義にしたがって詳しく書き下すと、以下のように 最高位の数字を求める方法 最高位の数字は、桁数を求める際に注目する10のn乗の小数部分に着目します。 (例題2):15 25 の最高位の数字と桁数を求めよ。 ただしlog 10 2= 、log 10 3= とする。 (解説2):まず常用対数を取ります。 log 10 15 25




平方根 とは 根号の意味や性質 値の求め方について 数学fun




二乗の期待値 未来の自分が読むメモ




3分で分かる 累乗根とは 定義や計算方法 公式 性質をどこよりも分かりやすく解説 合格サプリ



Www1 Iwate School Jp Action Common Download Main Upload Id 1371



高校の数学です 因数分解ですが 2乗の差を作るといわれてもなんのことやら Yahoo 知恵袋




因数分解の公式まとめ一覧とその活用例 アタリマエ
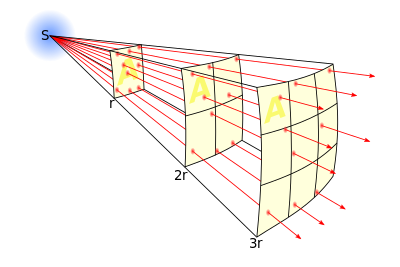



逆2乗の法則 Wikipedia




語呂合わせ 11の2乗 19の2乗までは暗記しよう 学習塾 Step By Step




自然数の2乗の求め方を知りたい こんにちは 数字がある数の2乗にな 数学 教えて Goo



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




2乗してはじめて0になる数 とかあったら面白くないですか ですよね アジマティクス




ルートの中に2乗があるとき すうがくのいえ




2乗してはじめて0になる数 とかあったら面白くないですか ですよね アジマティクス



Nの2乗を6で割ったときの余は 0か1か3か4であることを証明せよ と Yahoo 知恵袋




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




P乗を合計するための基本的な方法
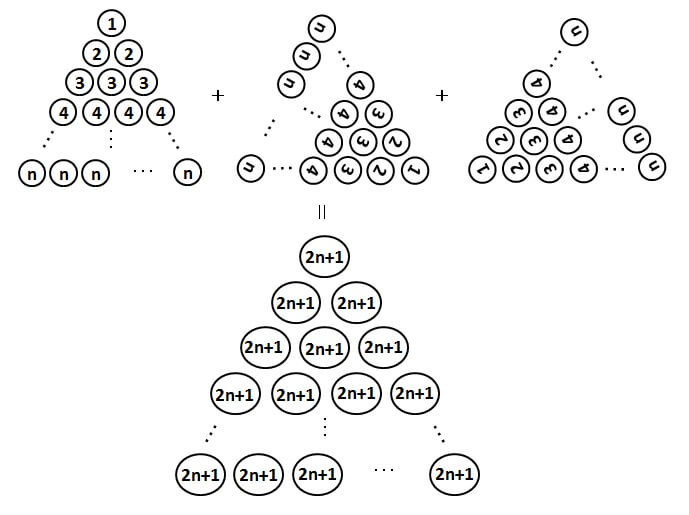



まとめ 2乗の和の公式の求め方 いろいろな方法をご紹介 ここからはじめる高校数学




シグマの公式 2乗 3乗 4乗 の証明は 数列の和はこれでマスター 東大医学部生の相談室



数学の問題です 十の位が5である2けたの自然数の2乗は速算で求めるこ Yahoo 知恵袋



Q Tbn And9gcqcddlbdlpx6ubpzbrdtzi 9xlahmsrygykxfaghpm2ng12vubg Usqp Cau




数学小話 いろいろ拡張しよう マイナス2分の1乗とは 日比谷高校のススメ




3分で分かる 累乗根とは 定義や計算方法 公式 性質をどこよりも分かりやすく解説 合格サプリ




中3数学 整数問題の証明2 連続する数 練習編 映像授業のtry It トライイット




60年解けなかった数学の難題 世界中のpcつなぎ解決 朝日新聞デジタル




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks



複素数とは 公式や I の 2 乗の意味 計算問題の解き方 受験辞典



Skの2乗の計算式




中3数学です Clear




ルート3が無理数であることを証明せよ 世界変動展望
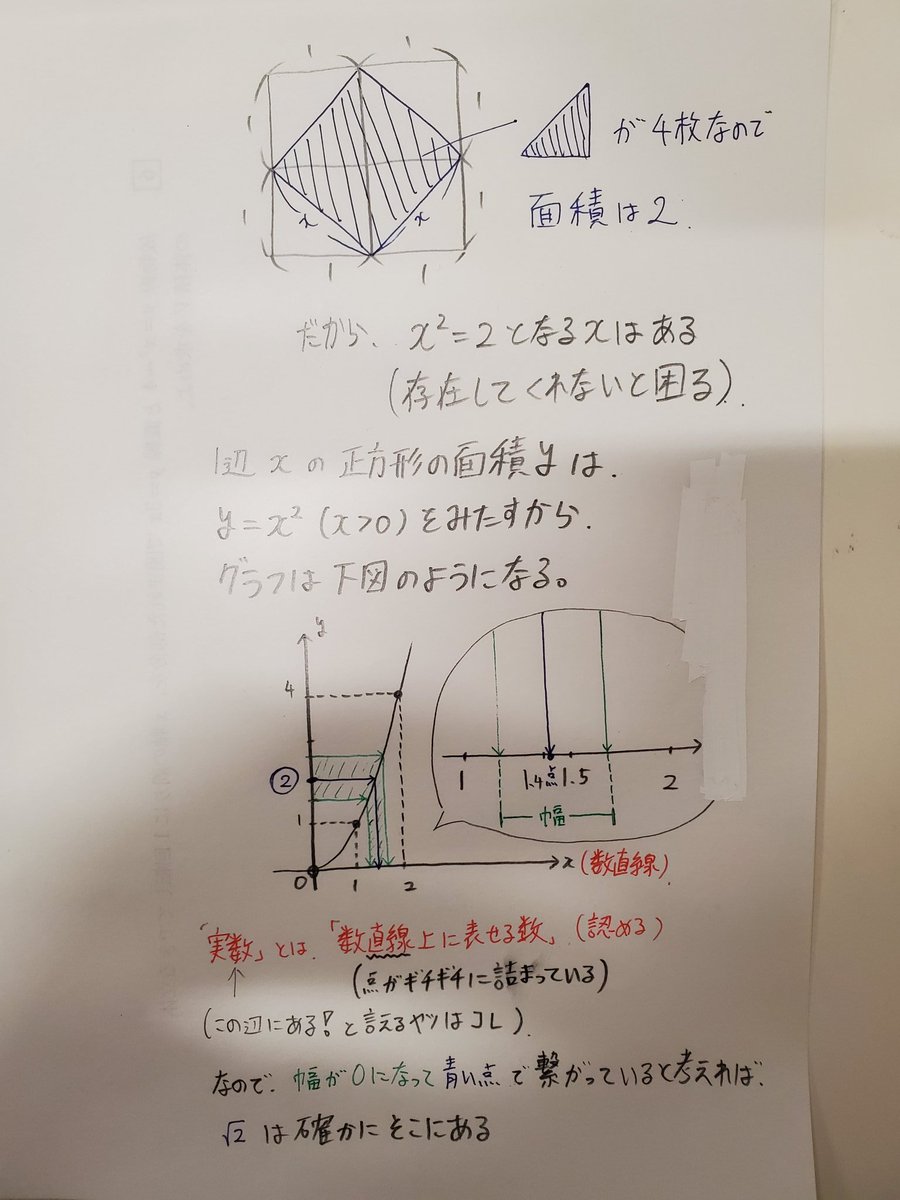



2 を2乗しても1 999 で 2にならないのでは 2は存在するのか 生徒の質問に答えようとする数学関係者一同の議論 Togetter




三乗の展開公式 A B 3乗の計算方法は 問題を使って解説 数スタ



数 分母に2乗があるときの部分分数分解 数学のコツ




実数の2乗は0以上 の使い方 数学 苦手解決q A 進研ゼミ高校講座
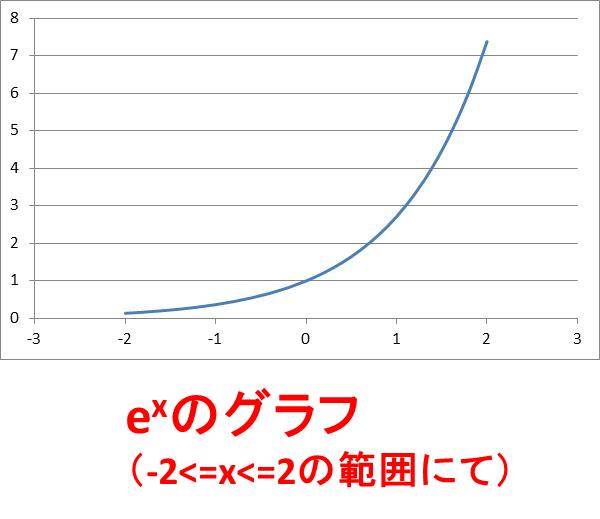



Eの0乗は値は何か Eの1乗やeのマイナス1乗 マイナス2乗の数値は y E 2xのe Xのグラフの書き方は エクセル ウルトラフリーダム




自乗と累乗 ベキ乗 理数系無料オンライン学習 Kori



数学的帰納法の問題で線引いてるところに変化する過程がわかりま Yahoo 知恵袋




6 375nの値が ある自然数の二乗となるような整数nのうち 最も小さいnの値を求 Clear
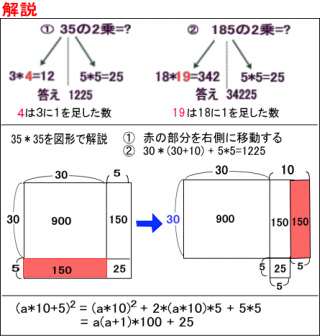



インド式2乗 下1桁が5の数 高精度計算サイト



数学的に 現実の世界で 何かを二乗するとはどういうことを意味しますか Quora




高校数学 数列 5 自然数の2乗の和 3乗の和 Youtube




なぜ2の0乗が1になるのか3分でわかりやすく解説 ハイパーメモメモ



数学的に 現実の世界で 何かを二乗するとはどういうことを意味しますか Quora




60年解けなかった数学の難題 世界中のpcつなぎ解決 朝日新聞デジタル



自乗と累乗 ベキ乗 理数系無料オンライン学習 Kori




なぜ Aの0乗は1 なのか その納得の理由を紹介します 数学の面白いこと 役に立つことをまとめたサイト



Q Tbn And9gctgepw5x8l1ei Otgt Oz9jn5qqqslmq4dpyziv5reqysmwysi3 Usqp Cau




中3数学 整数問題の証明2 連続する数 練習編 映像授業のtry It トライイット




1の位が5の数の2乗は1秒で計算できるよ Youtube




2乗してルートをつけると絶対値 数学の偏差値を上げて合格を目指す




高校数学a 累乗数の余りと下位桁の数を求める3つの方法 受験の月




インド式計算で1番最速で覚えやすいネタ おいしい数学




乗法公式 式の展開公式 19個まとめ 高校数学の美しい物語



累乗根



Meigaku Repo Nii Ac Jp Index Php Action Pages View Main Active Action Repository Action Common Download Item Id 3101 Item No 1 Attribute Id 18 File No 1 Page Id 13 Block Id 21
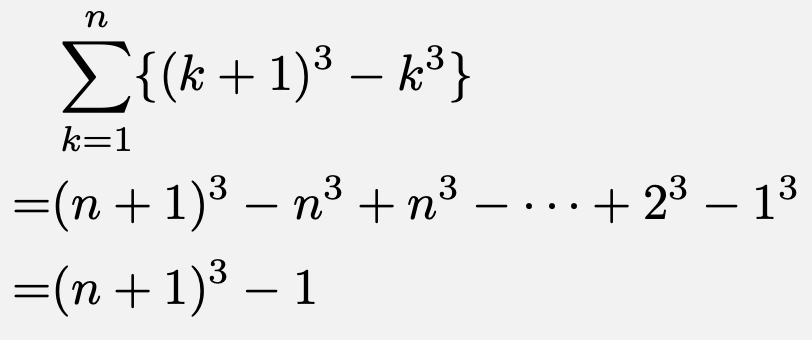



シグマの公式 2乗 3乗 4乗 の証明は 数列の和はこれでマスター 東大医学部生の相談室
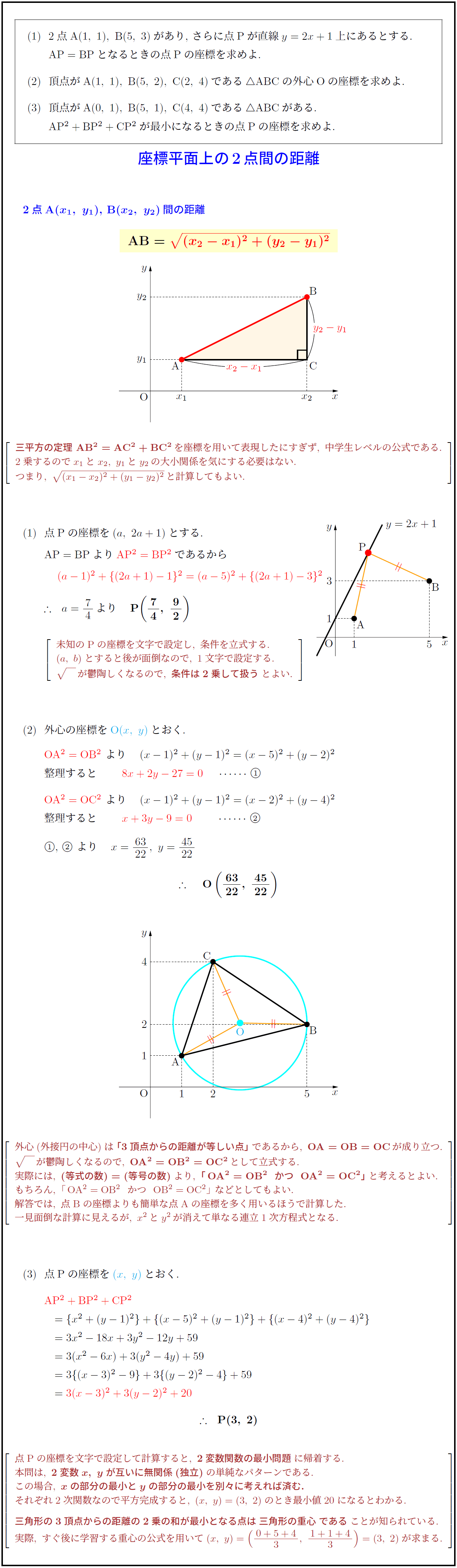



高校数学 座標平面上の2点間の距離 外心の座標 三角形の3頂点からの距離の2乗の和の最小 受験の月



2




小学3年生に A B の2乗と A B の2乗を教える方法 うさぎめし C




この問題で 5を証明するのがわかりません Clear




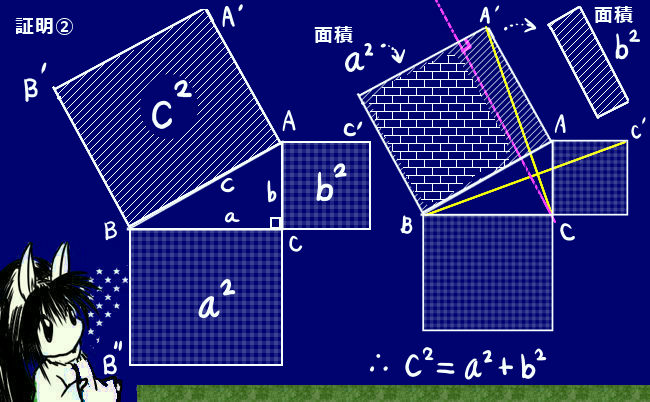
三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



Q Tbn And9gcsymbndgo2obahwwjzy0cnswmv6fyuw7arvj7arntyggu15 Naq Usqp Cau
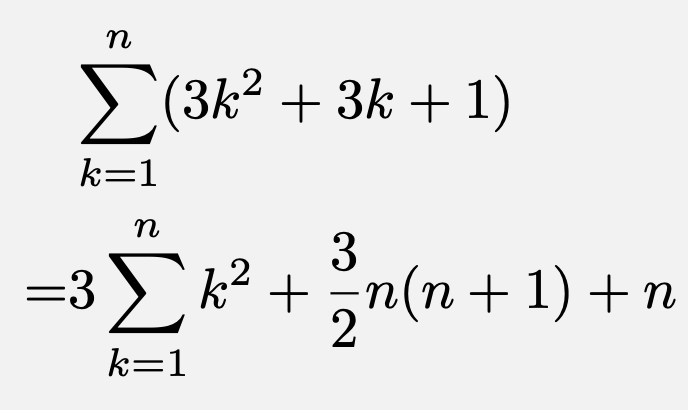



シグマの公式 2乗 3乗 4乗 の証明は 数列の和はこれでマスター 東大医学部生の相談室




数学を愛する会 無理数の無理数乗が有理数になるものはあるか 2 2が有理数ならばそれが1例 2 2が無理数ならば 2 2 2 2よりそれが1例




三乗の展開公式 A B 3乗の計算方法は 問題を使って解説 数スタ




2乗の展開 A B A B C A B C D 数学i 式の計算 1 Youtube




P乗を合計するための基本的な方法




2のルート2乗を卓上電卓で求める 怜悧玲瓏 高校数学を天空から俯瞰する




1 2乗って何 どうしてそれがルート 平方根 になるのか 数学の面白いこと 役に立つことをまとめたサイト




べき乗とは何か ゼロ乗 マイナス乗 分数乗 無理数乗ってどういう意味 アタリマエ
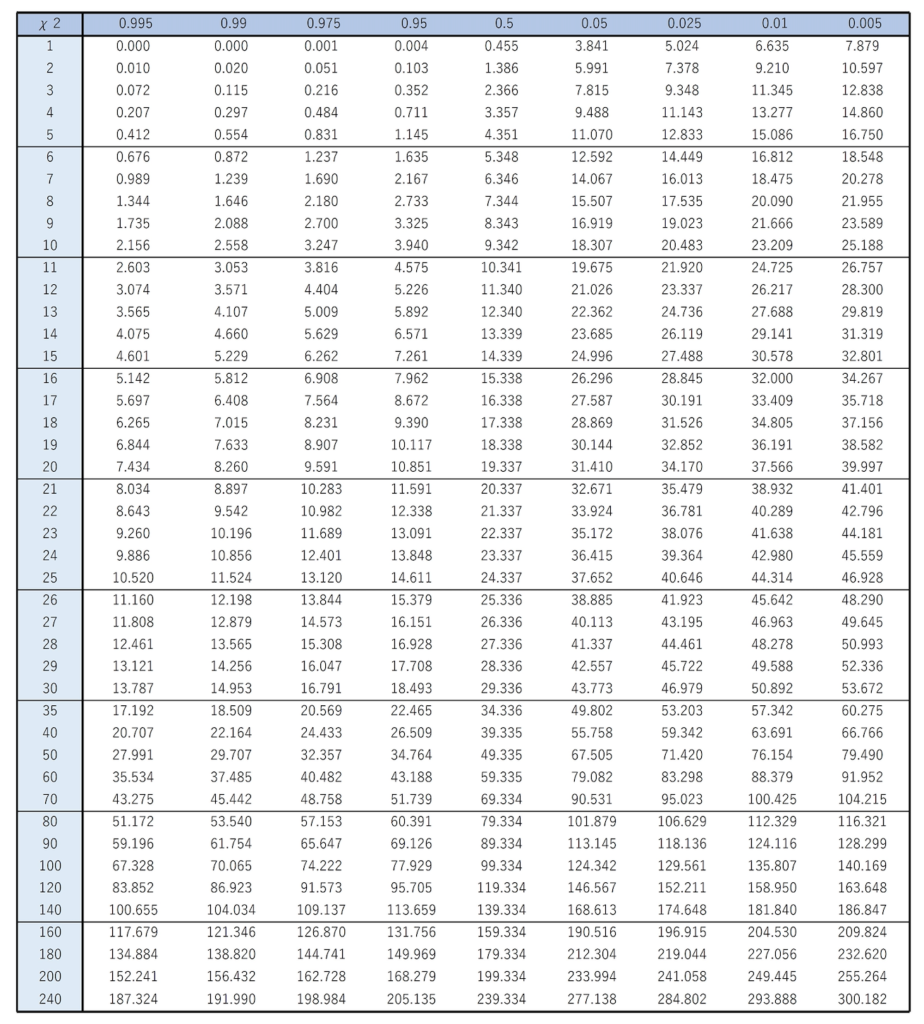



カイ二乗分布 中学の数学からはじめる統計検定2級講座第13回 とけたろうブログ




計算力が一気に上がる 速算術 計算の裏技 受験の月




ルート2乗 とは何か 高校教科書の指数拡張の話 Youtube




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ




インド式計算11選まとめてみた かけ算わり算や19 19までの九九や足し算など 遊ぶ数学
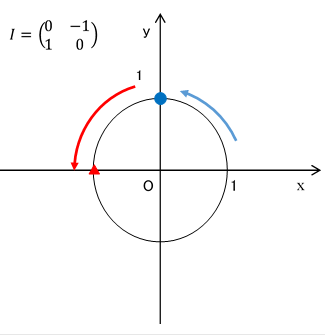



なぜ虚数単位iの2乗は 1になるのか




1000は2の何乗 は2の何乗 100万は2の何乗 ウルトラフリーダム




平方根の基本 無料で使える中学学習プリント




ルートの中に2乗があるとき すうがくのいえ



1 100までの二乗の計算 小学345塾
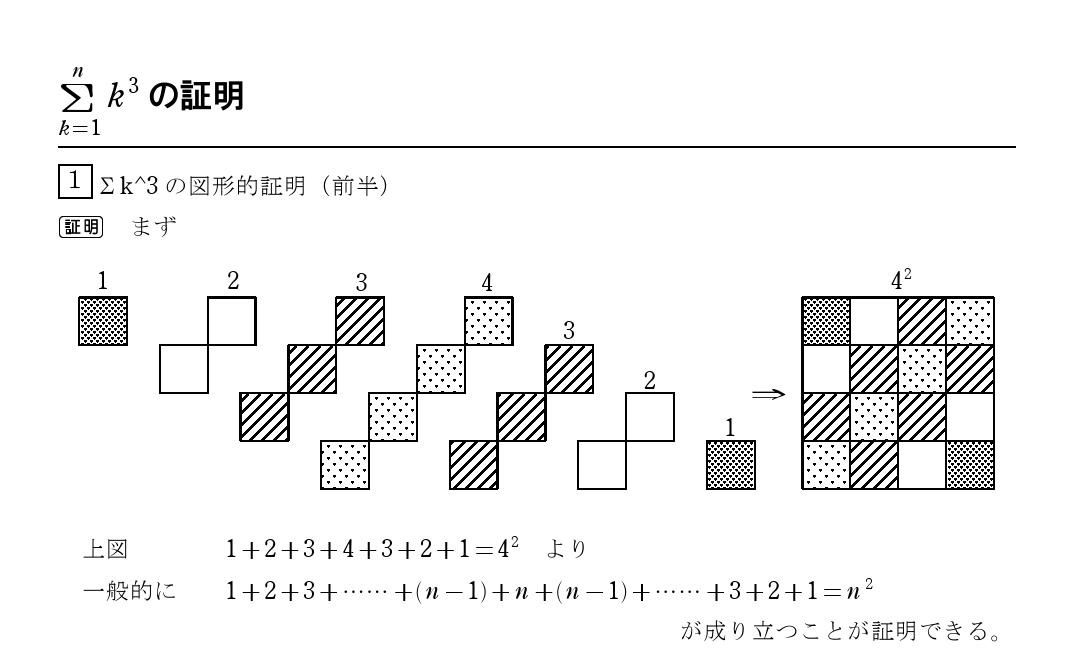



3乗和の公式の証明 怜悧玲瓏 高校数学を天空から俯瞰する




計算力が一気に上がる 速算術 計算の裏技 受験の月




下1桁が5の自然数の2乗 Fukusukeの数学めも




速算 二桁の整数の積を速く計算する方法 証明付き 大学入試数学の考え方と解法



熊先生の学習法



1 100までの二乗の計算 小学345塾




べき乗とは何か ゼロ乗 マイナス乗 分数乗 無理数乗ってどういう意味 アタリマエ




5乗和の公式の証明 怜悧玲瓏 高校数学を天空から俯瞰する




の部分はなぜ2乗するのですか Clear



0 件のコメント:
コメントを投稿