三平方定理 証明 247936-三平方定理 証明

三平方の定理には，いろいろな 証明方法があることが分かりま した。とても驚きました。 三平方の定理の逆が成り立てば， 直角三角形なんだということが 分かった。どの辺を斜辺と考え たらいいのか， さんに説明 してもらったので納得できまし た。既に回答があるように, 三平方の定理は数多く知られています。しかし, 三平方の定理があまりにも基本的な性質なので, 変わった証明を考えるのは困難です。変わったことをしようとすると, 実は三平方の定理がなければ導けない事実を使ってしまうことがあるからです。を満たす．この m, n に順次整数を入れていけば三平方の定理を満たす3つの整数を無限にたくさん見つけられる． \( 3^24^2=5^2 \) \( 5^212^2=13^2 \) \( 8^215^2=17^2 \) \( ^221^2=29^2 \) \( 9^240^2=41^2 \) \( 12^235^2=37^2 \) \( 11^260^2=61^2 \) 古代ギリシャのディオファントスはこうしたことをたくさん調べて「算術

勾股定理逆定理的证明过程 初三网

三平方定理 証明

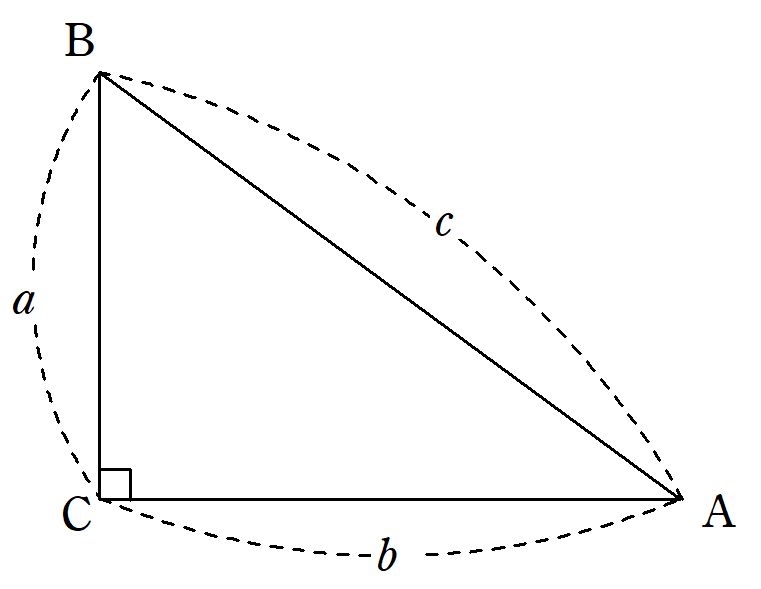
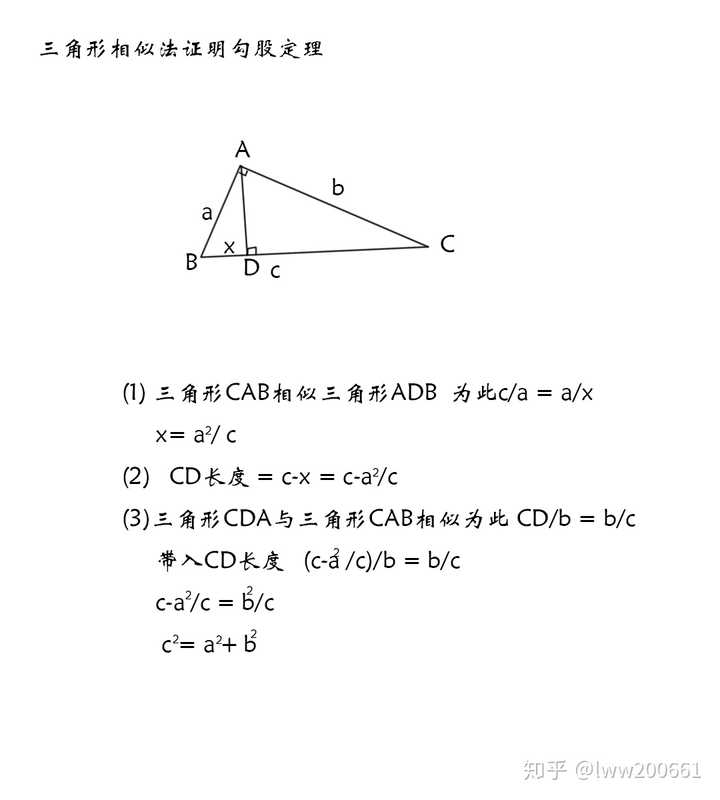
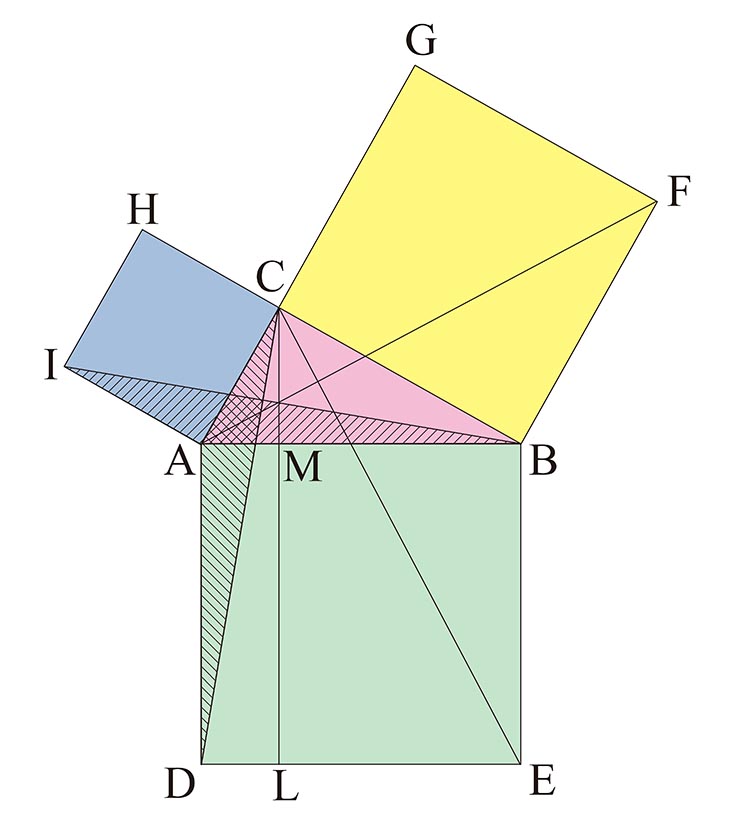
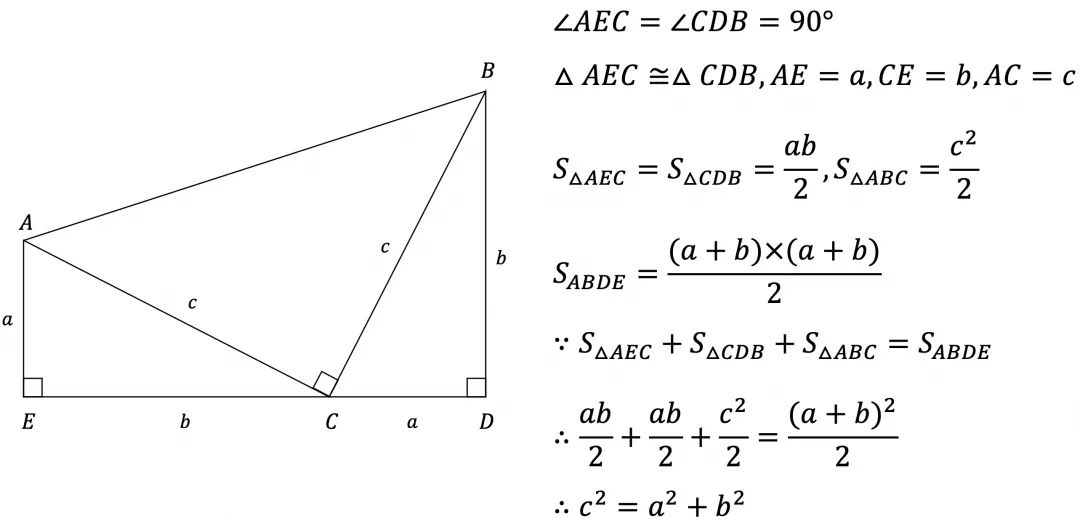
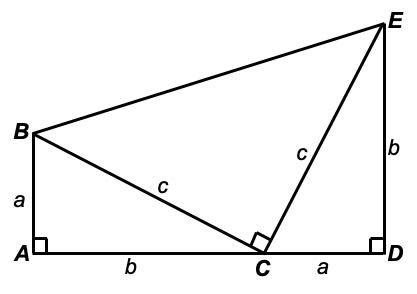
三平方定理 証明-このピタゴラスの定理（三平方の定理）の証明は、百以上知られている。その全てを紹 介することは困難であるが、定理が成り立つことを納得する一つの方法として、その証明 のいくつかに触れることは今後の学習において有効と考える。 当HPがいつもお世話になっている未菜実さんからの三平方の定理の証明 直角三角形の角から斜辺と垂直な直線を引いて、直角三角形を二つに分ける。すると、もとの直角三角形と新しく中にできた直角三角形が相似の関係になる。 相似は二組ある。三角形の二角が一致すれば相似になることを思い出そう。 この二組の相似から \ ca=ax\\ a^2=cx

勾股定理证明方法欣赏 2

立体の表面積展開図（入試問題） → 携帯版は別頁 《解説》 次のような直角三角形の三辺の長さについては， a 2b 2=c 2 が成り立ちます．（これを三平方の定理といいます．） 逆に，三辺の長さについて， a 2b 2=c 2 が成り立つとき，その三角形は直角三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。三平方の定理の証明 いろいろな種類40通りの証明を行いました。 丁寧とはいえない書き方のものもありますが、各自補って読んでください。 三角形や四角形の面積（等積変形など）を用いているもの、三角形の相似を用いているもの、 別の定理を証明したのちそれを用いているものなど

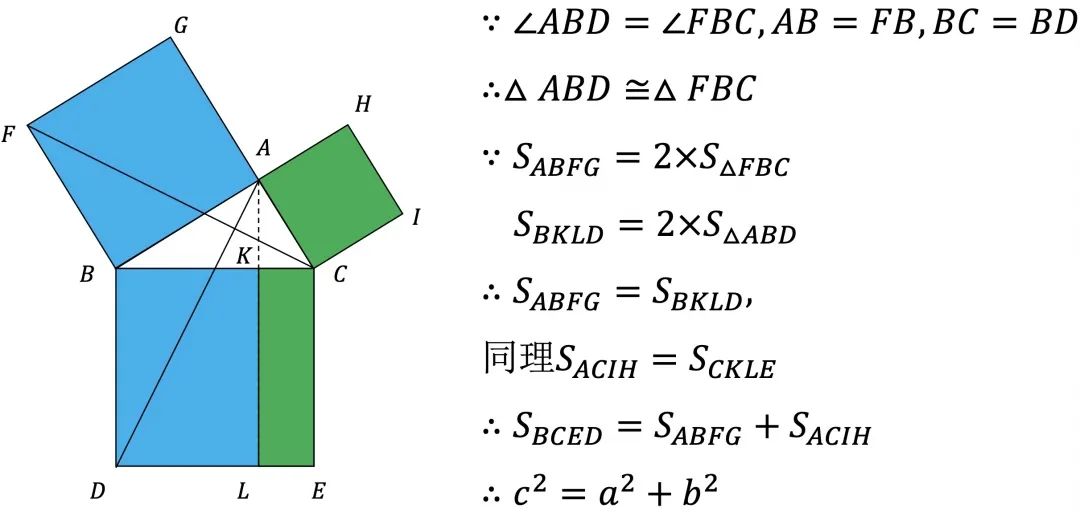
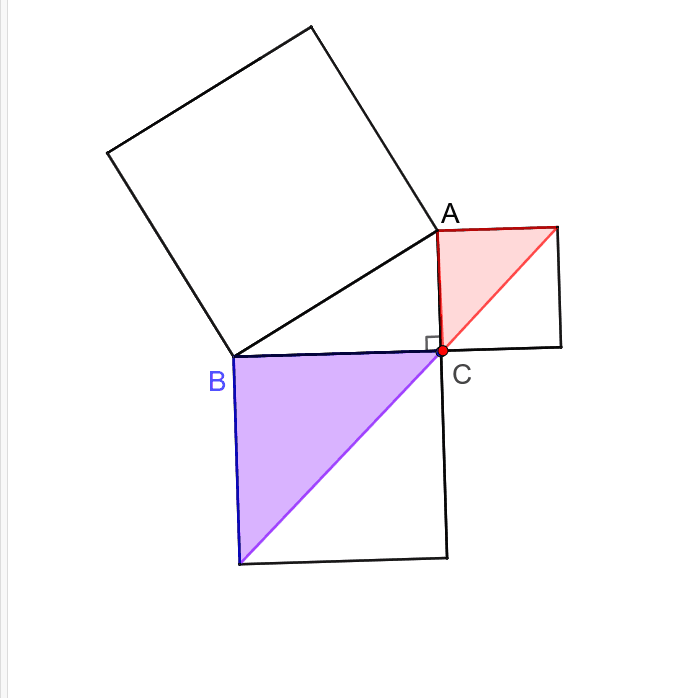
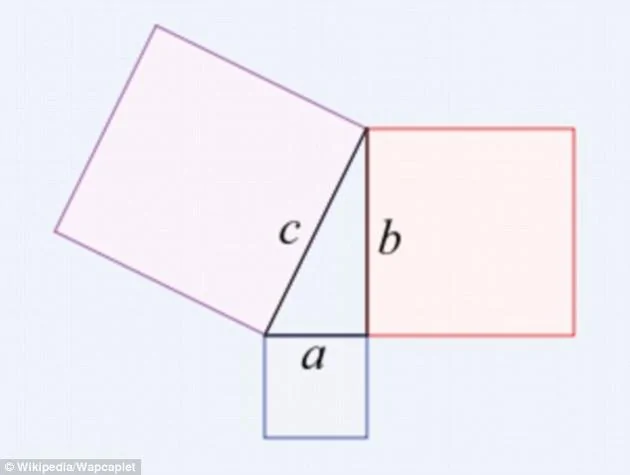
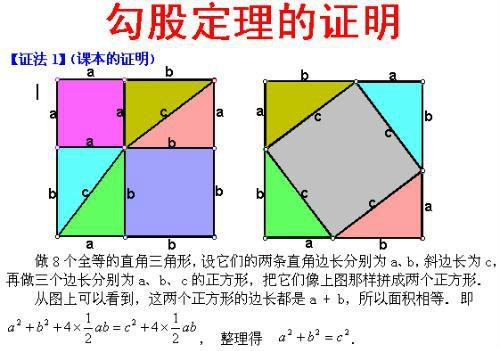
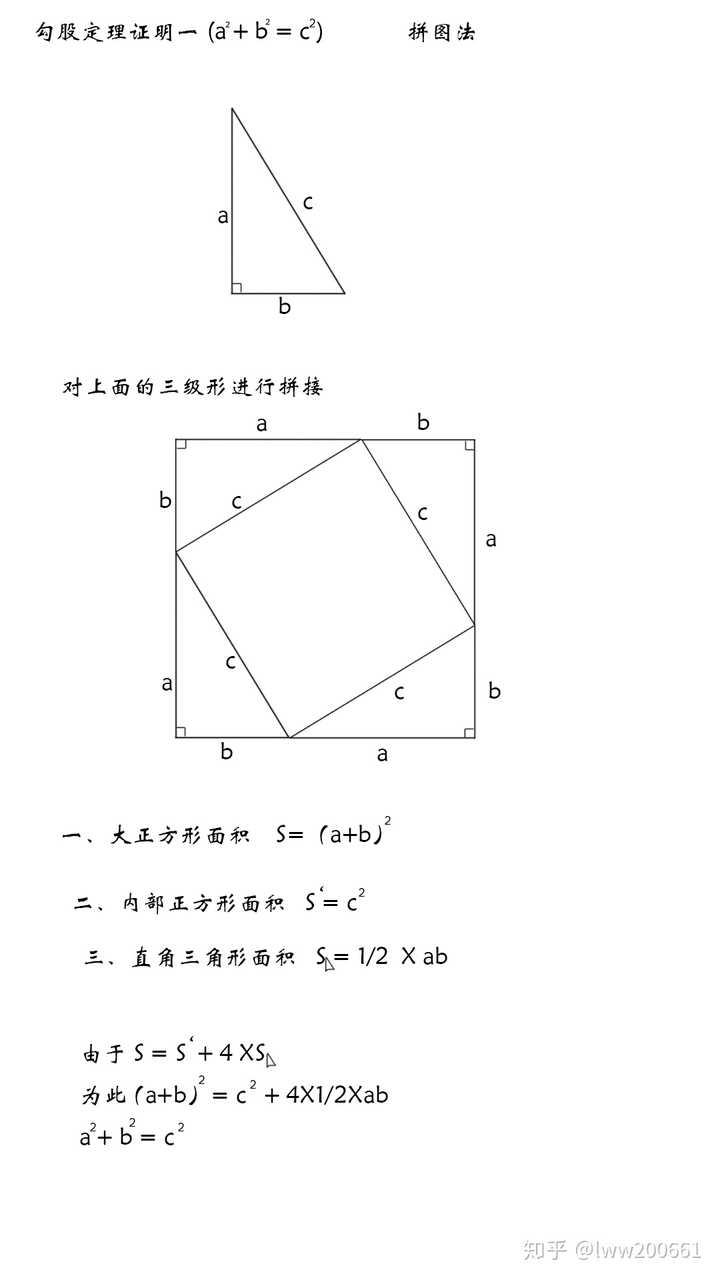
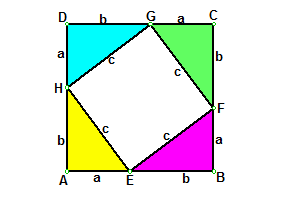
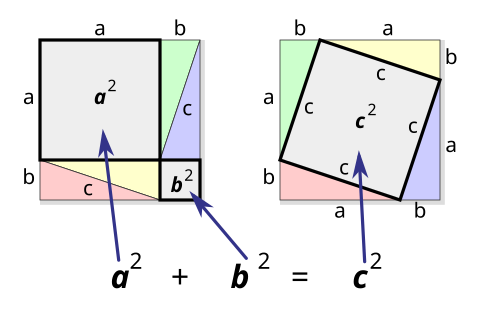
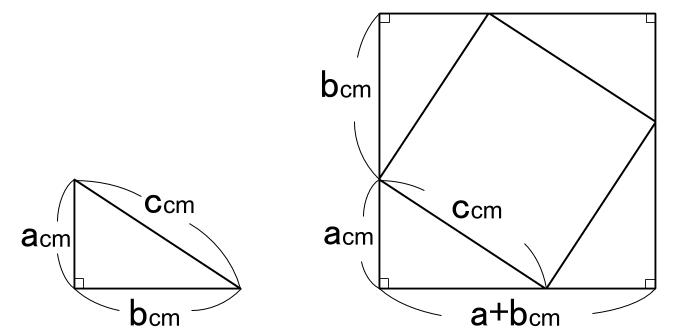
三平方の定理の証明＜６＞ 太線の正方形の面積を (ｱ)外側の１辺×１辺と考えると (a＋b)2 (ｲ)cを1 辺とする正方形の面積と 4 つの直角三角形の面積の 合計と考えると c2＋a×b××4 (ｳ)(ｱ)と(ｲ)は同じ面積を表しているので (a＋b)2＝c2＋2abしたがって，a2＋b2＝c2三平方の定理 三平方の定理(1) 1 次の図でxの値を求めなさい。 374 3㎝ 4㎝ 三平方の定理より x ＝4 ＋3 ＝16＋9 ＝ x ＞0だから x ＝ 答え x 2 2 2 2 次の図でxの値を求めなさい。 3 次の長方形の対角線の長さを求めなさい。 対角線の長さをx ㎝とすると 三平方の定理より、三平方の定理 （さんへいほうのていり）、 勾股弦の定理 （こうこげんのていり）とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。

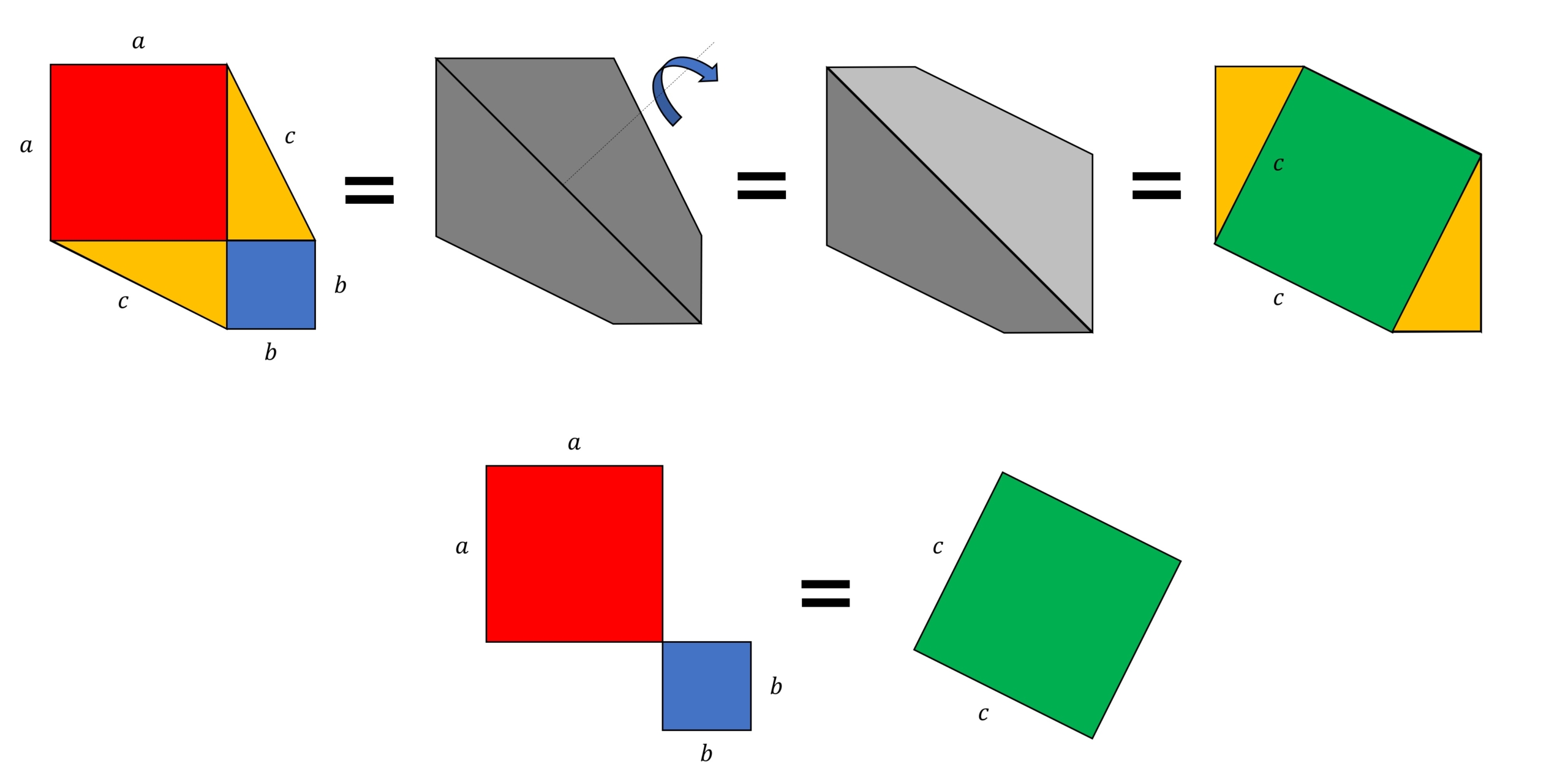
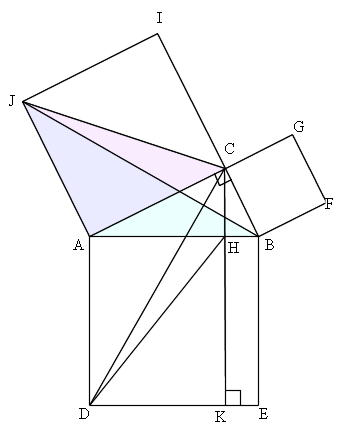
 ですから， 余弦定理の場合は − 2 b c cos ⁡ θ の項が三平方の定理に付け加えられているだけですね． つまり， ∠ A が 90 ∘ から θ に変わると，三平方の定理の等式が − 2 b c cos ⁡ θ 分だけズレるということになっているわけです． このように見る三平方の定理を文字で起こしてみるとこんな感じ。 3辺の長さ \(a, b, c(斜辺)\) とする直角三角形ならば、\(c^2=a^2b^2\) が成り立つ これを逆にしたものを三平方の定理の証明＜2C＞ 三平方の定理の証明＜3＞ （アインシュタインが小学生の時に見つけたといわれる証明） AB BC CA＝ ， ＝ ， ＝ とするとc a b ∽ ∽ となりABC CBD ACD 斜辺の長さを利用して 相似比は ： ：c a b 面積比＝(相似比) なので2 面積比は ： ：c a b2 2 2 の面積＝ の面積＋ の面

勾股定理证明最简单的自己想的

1

三平方の定理の証明 三平方の定理はなぜ成立するのか。 ありとあらゆる直角三角形に成り立つというのです。不思議な気がしませんか？ 実に様々な証明がありますが、 中学生が学習しておくべき最も重要な証明を紹介します。 三平方の例 (1) 1 2 x 斜辺がxなので 1 2 2 2 =x 2 x 2 = 5 x > 0 より 1．三平方の定理の証明その1 まずは良く知られた、最もポピュラー（？）な証明方法をご紹介します。 まず、直角三角形abcを準備します。長さが𝑎と𝑏（𝑎>𝑏とします）、斜辺を𝑐としましょう。以降、この直角三角形をベースにお話していきます。 まずはこの三角形を4

三平方の定理の証明 ピタゴラスの証明 Fukusukeの数学めも

ピタゴラスの定理とその証明

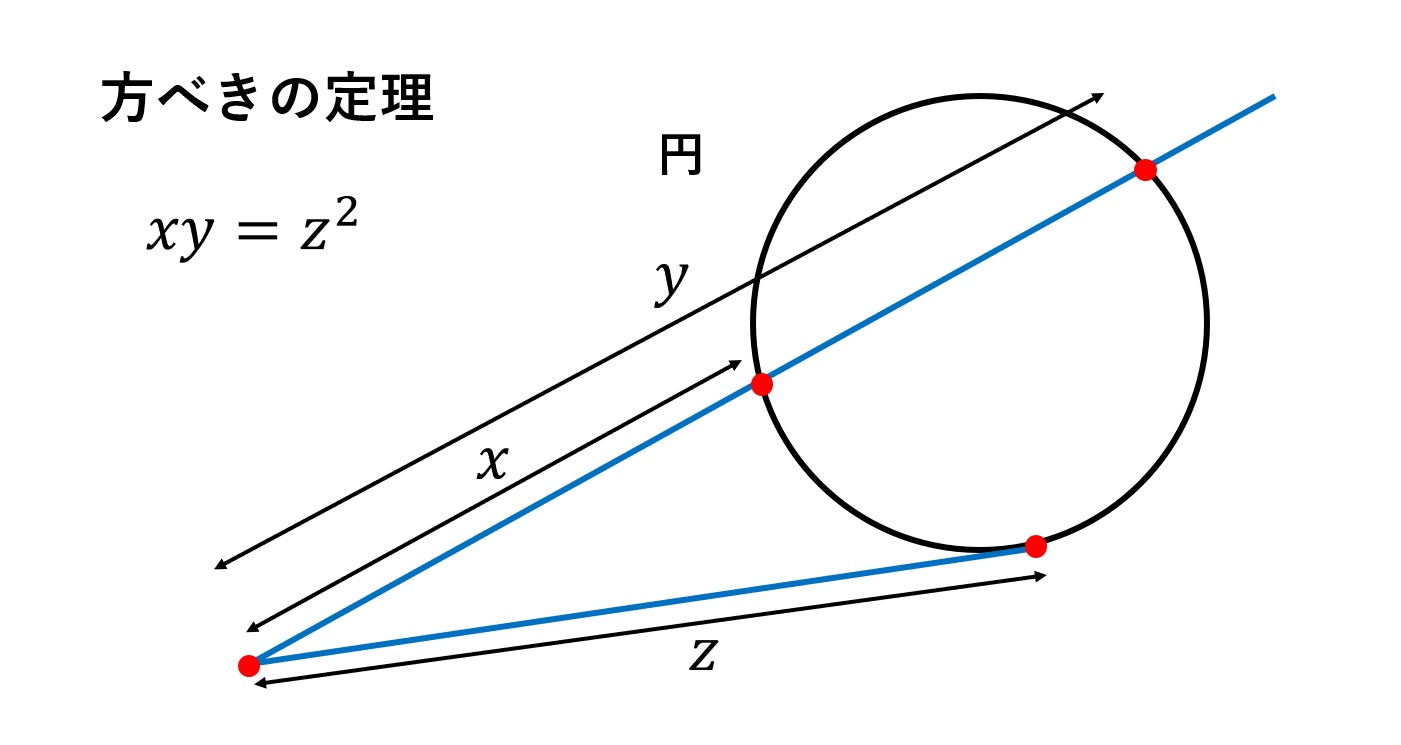
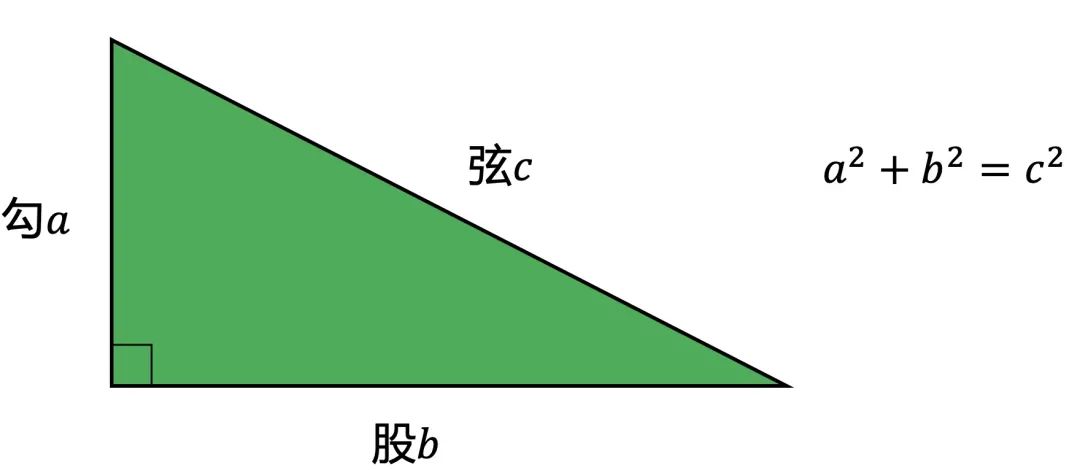
日本大百科全書(ニッポニカ) 三平方の定理の用語解説 直角三角形abcが与えられたとき、斜辺bcを1辺とする正方形の面積は、他の2辺ab、acを1辺とする二つの正方形の面積の和に等しい。すなわち、 bc2＝ab2＋ac2が成立する。これを三平方の定理という。 三平方の定理には数百もの証明方法があります。接線型の方べきの定理を利用した証明を 接線型の方べきの定理を利用した証明を 三角形の辺と角の大小ピタゴラスの定理の証明を集めた本は多数あるが，今回の記事を書くにあたり，『ピタゴラスの定理 $100$ の証明法 ― 幾何の散歩道』（森下四郎著，プレアデス出版）を参考にした．証明が種類別に分けられ，系統的に説明されていて分かりやすい．考えていて楽しくなるような，趣向を凝らし

勾股定理证明方法欣赏 2

数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube

直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係はピタゴラスの定理（三平方の定理）と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス(cBC570cBC500)が発見したかどうか確証があるわけではありません。この三平方の定理の証明は中学校の教科書に載っているそうです (10 年 1 月)。 中学校の教科書にある図は 1 辺が ab の正方形と 2 辺が a, b の直角三角形 4 個が 描かれているようです。つまり上の図の外側の部分だけです。 またこの証明は古代インドの数学者かつ天文学者でもあるアリヤ三平方の定理の証明方沵は数百通りを数えるといわれている。上に上げた例は視覚的に捉えや すいものを扱った。このほかの方沵も暯物ン゜ルシヅセダなどで多数紹介されている。証明方沵 の発見者のハュネ゛ヴャにも様々なものがあり過去から現在に至るまで多くの人をひきつけた定 理で

四平方和定理 搜索结果 哔哩哔哩 Bilibili

悟空问答 勾股定理有什么神奇的证明方法 25个回答

 ヒポクラテスの定理（ヒポクラテスのていり、英語 Hippocrates's theorem ）とは、幾何学の定理である。 ヒポクラテスの三日月（ lune of Hippocrates ）ともいう。 ヒオスのヒポクラテス （英語版） に因んで名づけられた。 数学的に計算された正確な面積を持つ最初の曲線図である。 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。 ピタゴラスの定理（三平方の定理）を使うと， a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 を満たす自然数の組 (a, b, c) (a,b,c) (a, b, c) をピタゴラス数と呼ぶ。 と言うこともできます。 例えば， 3 2 4 2 = 5 2 3^24^2=5^2 3 2 4 2 = 5 2 なので (3, 4, 5) (3,4,5) (3, 4, 5) はピタゴラス数です。 他にも， 5 2 1 2 2 = 1 3 2 5^212^2=13^2 5 2 1 2 2 = 1 3 2

勾股定理竟然有500种证明方法 你会几种 技术圈

勾股定理及勾股定理的逆定理

 どこまで、『三平方の定理の証明』を調べるか？ 僕個人では、3通りの証明を、自分の中に体取、体得でき、その細部をこうして表現出来れば良いかと考えた。 此処まで、2通りの証明を紹介した。 1、等積変形に依る三平方の定理の証明 2、4枚の合同な直角三角形の配置の仕方に依る証明三平方の定理の証明には他にも様々な方法がある。 証明2 証明3 三平方の定理の使い方 直角三角形の2辺がわかっている場合、三平方の定理を用いて残りの1辺を出すことが出来る。 どれが斜辺になるかを間違えないように注意する!!

Q Tbn And9gcr Zdue Nx7dskj6j9hsup G7flm30r5ual62zlaad3em Pb6xz Usqp Cau

勾股定理 从证明到简单应用 小学奥数 知乎

勾股定理逆定理的证明过程 初三网

暑假提升攻略 余弦定理的十种证明方法 值得收藏 雪花新闻

Amc 10 第二讲 符合勾股定理的所有整数 都画在坐标系中是什么样 知乎

如何证明勾股定理 知乎

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

三平方の定理の証明 ユークリッドの証明 Geogebra

最长数学证明破解世界难题 全部阅读需100亿年 阿波罗新闻网

数三考费马引理吗 费马大定理证明过程 高中生证明费马大定理

素数中的数学知识 费马二平方定理 费马 定理 欧拉 数学 素数 手机网易网

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

勾股定理怎么算 科普 常识知识

三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ

初中数学 勾股定理的多种证明

勾股定理的证明方法是什么 高三网

Amc10 勾股定理中的乐趣有多少

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

畢氏定理by Mblab316 Issuu

中学数学 三平方の定理

1

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張

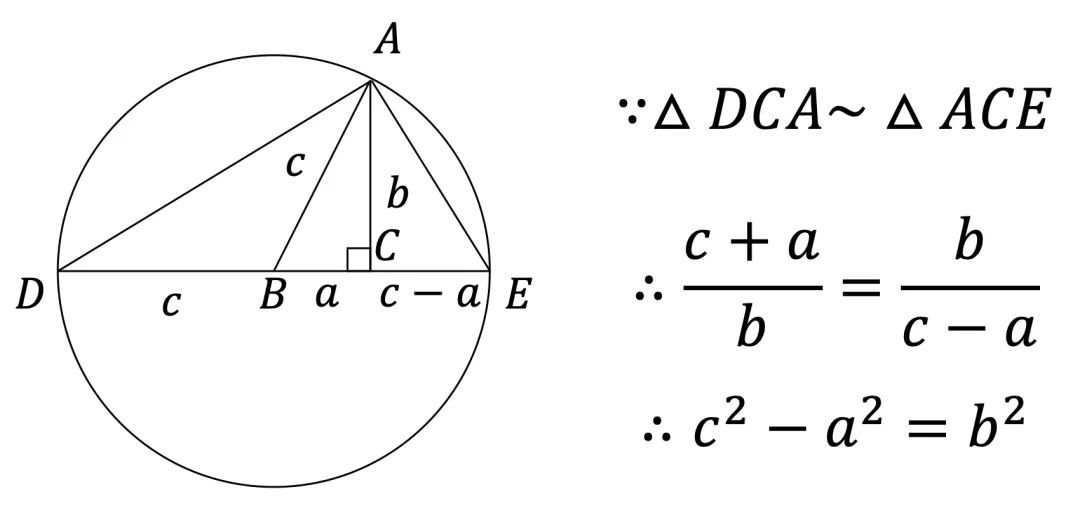
勾股定理竟然有500种证明方法 你会几种 技术圈

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

如何证明勾股定理 知乎

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理

三平方の定理の最も変わった証明方法はなんですか Quora

勾股定理的证明方法有多少种

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

常见勾股定理的证明方法有哪些 如何证明勾股定理 星火网校

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション

证明之书 第四问 哪些数可以被写成两个数的平方和 哔哩哔哩

勾股定理的证明方法汇总一

如何学好初中数学 海伦公式及其证明 三角形

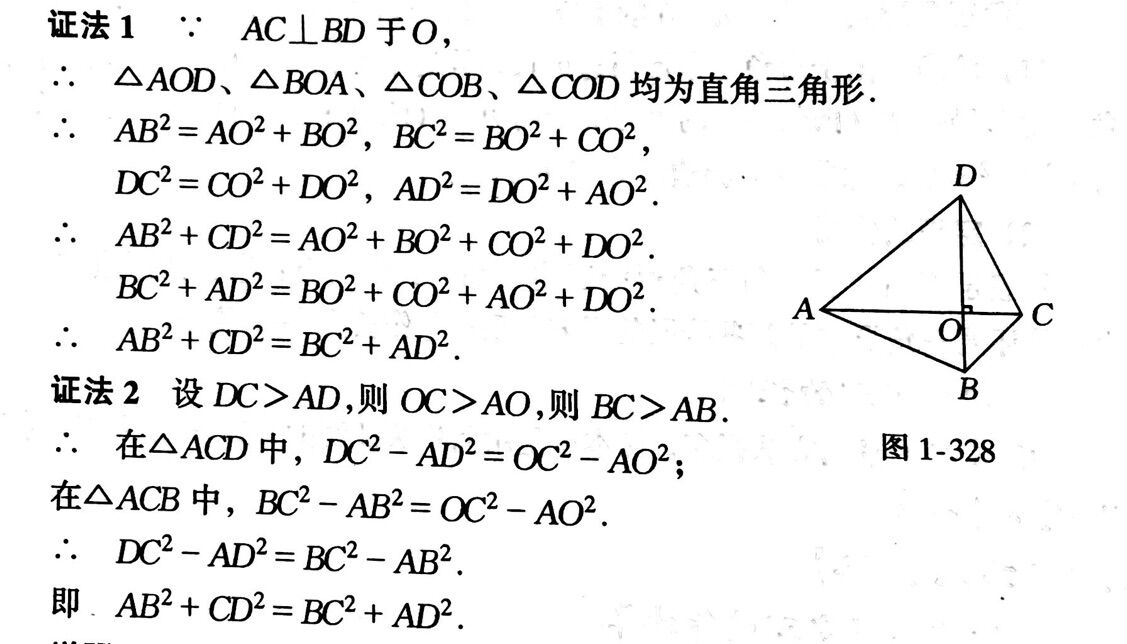
斜边中线定理如何证明直角三角形斜边中线定理 不要涉及高中知识 朵拉利品网

少有人走的路 三角函数超入门 1 三平方定理的证明

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

五合一定理 每日头条

三平方の定理

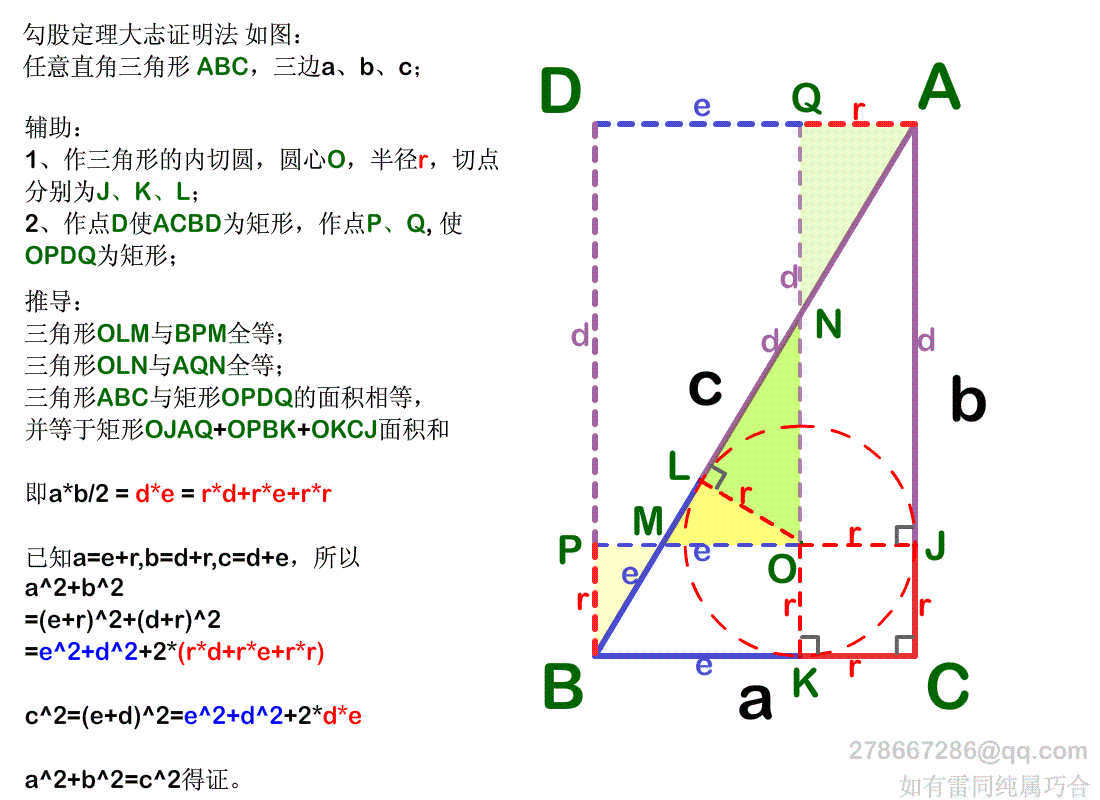
一不小心 发现个勾股定理证明方法 大志的博客 Csdn博客 勾股定理证明

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

三平方の定理 証明 Pythagorean Theorem Proof With English Subtitles Youtube

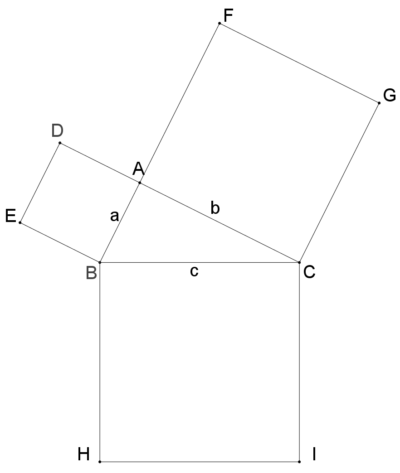
三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも

初中数学 毕氏定理 维基教科书 自由的教学读本

勾股定理的证明方法图 勾股定理数学多种证明方法 共2篇 尚书坊

三平方の定理について考える１ 教科書 大日本図書 の証明方法 身勝手な主張

Amc10 勾股定理中的乐趣有多少

三角形勾股定理公式及证明方法 初三网

勾股定理在空间中的类推 知乎

勾股定理竟然有500种证明方法 你会几种 技术圈

三平方の定理の４通りの美しい証明 高校数学の美しい物語

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4

勾股定理证明最简单的方法 初三网

三平方の定理

Mathematics 三平方の定理 １ 三平方の定理の証明 働きアリ

ポテト一郎 三平方の定理 一番好きな証明です

三平方の定理の証明 直感的に分かる図で解説します 数学fun

三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori

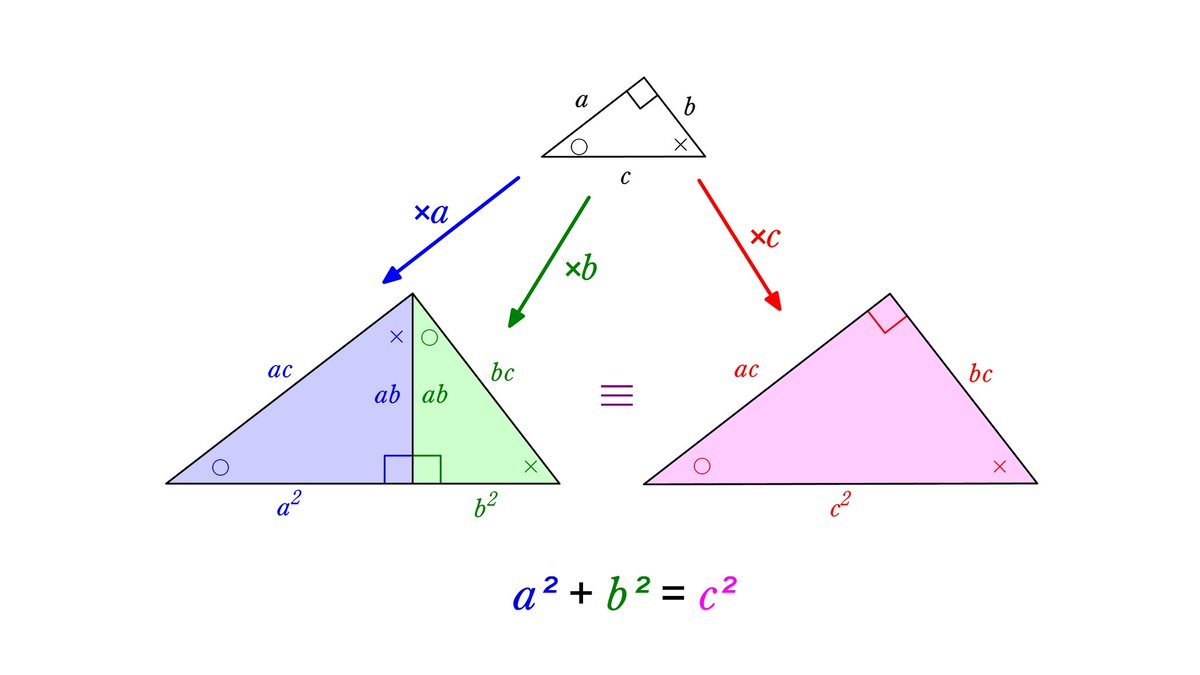
勾股定理竟然有500种证明方法 你会几种 技术圈

中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su

初中数学勾股定理公式大全 初三网

三平方の定理について考える４ 三角形の相似を使った証明方法 身勝手な主張

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記

三平方の定理の証明と使い方

射影定理 维基百科 自由的百科全书

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

海伦公式 维基百科 自由的百科全书

中3no三平方の定理3 Youtube

三平方の定理の証明 方べきの定理の利用１ Fukusukeの数学めも

三平方の定理の４通りの美しい証明 高校数学の美しい物語

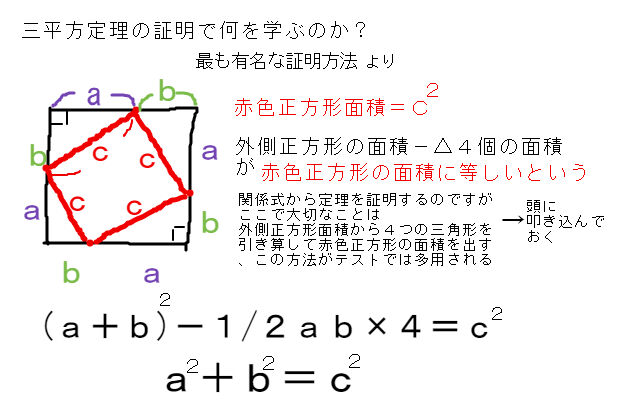
三平方定理の証明内容で最も覚えておくべきこと 中学数学 理科 寺子屋塾の復習サイト

Q Tbn And9gcrw1rs7aetaptn1yxqopgmw7u4dsyyhdm2d15yznhw4vshjwes0 Usqp Cau

ピタゴラスの定理 の証明アニメ6 ユークリッド Youtube

少有人走的路 三角函数超入门 1 三平方定理的证明

史上最无聊的高考数学题 Steemit

三平方の定理

三平方の定理の証明 ブリリアンス数学 Youtube

证明之书 第四问 哪些数可以被写成两个数的平方和 哔哩哔哩

三平方の定理

证明之书 第四问 哪些数可以被写成两个数的平方和 哔哩哔哩

中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

老師不教的數學 畢氏定理 Pythagorean Theorem 的証明 Gif動圖詳解 中二識用 小五可試 經數樂園 學習變有趣 A Href Ronaldchik Blogspot Com P Econ Math Lesson Html 要補習 A

中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su

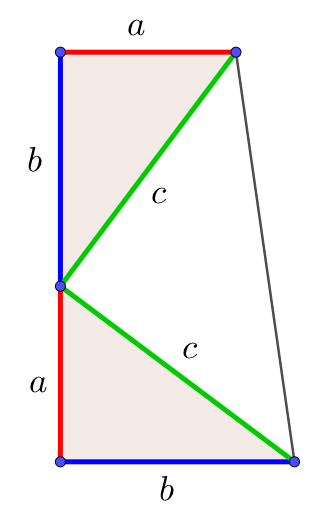
三平方の定理の証明３ 大統領の台形 キソカラ

ピタゴラスの定理 三平方の定理 の証明 Geogebra

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

我国数学教材中的 勾股定理 是否应该改成 毕达哥拉斯定理 Pythagoras Theorem 知乎

Incoming Term: 三平方定理 証明,